Natural Projection Homomorphisms Have Kernels That Are Easy to Find!

preview_player
Показать описание
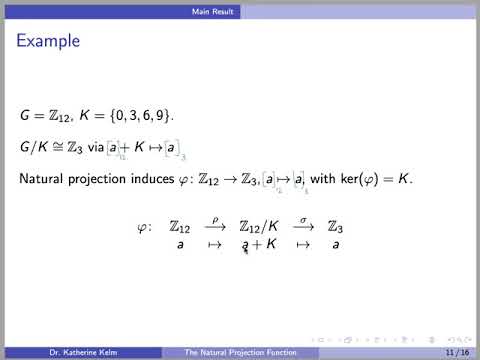
In Ring Theory from Abstract Algebra, let R be a ring and let A be a (two-sided) ideal of R. The natural projection mapping π: R → R/A from the ring R to the factor ring (a.k.a. quotient ring) R/A is an onto homomorphism (we also say it is a surjection and an epimorphism). This function is defined by the formula π(r) = r + A, where r + A is the left coset of A in R containing r. What is the kernel of this natural mapping? It is the ideal A itself!

#AbstractAlgebra #RingTheory #homomorphism #FactorRing #QuotientRing

Links and resources
===============================

AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
  1. Bill Kinney
  2. abstract algebra
  3. ring theory
  4. group theory
  5. projection
  6. projection homomorphism
Рекомендации по теме
Natural Projection Homomorphisms 0:08:10

Natural Projection Homomorphisms Have Kernels That Are Easy to Find!

Kernels, Homomorphisms, and 0:20:24

Kernels, Homomorphisms, and the Natural Projection Function

Any Ideal A 0:09:03

Any Ideal A in R is the Kernel of the Natural Projection Ring Homomorphism onto the Factor Ring R/A

Let's Explore Homomorphisms, 0:34:40

Let's Explore Homomorphisms, Kernels, and the First Isomorphism Theorem! 😀

Abstract Alg, Lec 0:36:50

Abstract Alg, Lec 21A: Internal Direct Products, Homomorphisms, Kernels, First Isomorphism Theorem

canonical/natural homomorphism in 0:02:58

canonical/natural homomorphism in ring theory

Ring Homomorphisms | 1:13:02

Ring Homomorphisms | Modern Algebra

Group, Lec.- 50(Kernel 0:40:08

Group, Lec.- 50(Kernel of a Homomorphism), by Dr.D.N.Garain, for B.Sc/M.Sc(Maths.)

Abstract Algebra: Exam 0:58:58

Abstract Algebra: Exam 2 Review (Group Homomorphisms, Kernels, Preimages, Factor Groups)

Kernel | Kernel 0:47:57

Kernel | Kernel is an ideal proof | Property of Ring Homomorphism | TYBSc | Ring Theory

Tangent Space to 0:01:44

Tangent Space to Submanifolds (part 2)- as kernel of projection map

Natural homomorphism theorem 0:04:12

Natural homomorphism theorem

#26: Bence Horváth- 0:54:12

#26: Bence Horváth- When are surjective algebra homomorphisms of B(X) automatically injective?

Group Theory: 08 1:06:32

Group Theory: 08 Homomorphisms, Conjugacy

Algebra class 30 0:14:51

Algebra class 30 - Homomorphism of rings: Dr. Shikhi M

9.9 Associated matrix 0:07:14

9.9 Associated matrix to a composition of homomorphisms - Linear Algebra and Analytic Geometry

Ring Homomorphisms (Gallian 0:58:51

Ring Homomorphisms (Gallian Chapter 15)

#41: Bill Johnson- 1:02:18

#41: Bill Johnson- Homomorphisms from L(l_p) and L(L_p)

Fermat's Last Theorem: 0:04:27

Fermat's Last Theorem: Group Objects and Homomorphisms! (5.3, 69)

301.10G Extra: First 0:09:39

301.10G Extra: First Isomorphism Theorem - Linear Algebra

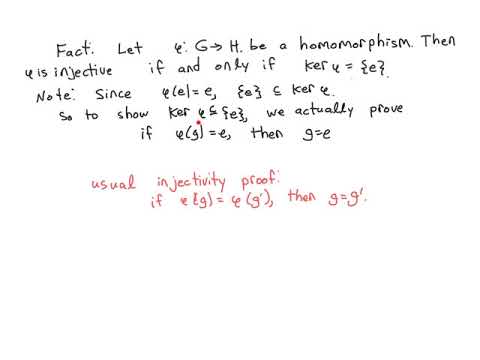kernel properties 0:15:25

kernel properties

Normal subgroups and 0:14:53

Normal subgroups and quotient groups

Abstract Algeba: L25, 0:52:21

Abstract Algeba: L25, ring homomorphism, 11-4-16

23-Homomorphisms of Rings 0:37:10

23-Homomorphisms of Rings