filmov
tv
Chirality VS. Helicity | Spin and Lorentz Group

Показать описание
Chirality and helicity often appear at the same time in a lecture and often it’s difficult to figure out their difference. So what exactly is the difference between chirality and helicity?
If you want to read more about helicity and chirality, we can recommend the book „An Introduction to Quantum Field Theory“ by Michael Peskin and Daniel Schroeder:
(Affiliate-Link)
Table of Contents:
00:00 Spin
00:56 Helicity
02:50 Chirality
03:52 Representations of the Lorentz Group
05:21 Connection to the Standard Model of Particle Physics
#ParticlePhysics #QuantumMechanics #Relativity
If you want to help us get rid of ads on YouTube, you can support us on Patreon!
If you want to read more about helicity and chirality, we can recommend the book „An Introduction to Quantum Field Theory“ by Michael Peskin and Daniel Schroeder:
(Affiliate-Link)
Table of Contents:
00:00 Spin
00:56 Helicity
02:50 Chirality
03:52 Representations of the Lorentz Group
05:21 Connection to the Standard Model of Particle Physics
#ParticlePhysics #QuantumMechanics #Relativity
If you want to help us get rid of ads on YouTube, you can support us on Patreon!
Chirality VS. Helicity | Spin and Lorentz Group
Chirality|Basic Concept Explained
Maxim Chernodub, Helicity vs. chirality: transport, thermodynamic, and spin-polarization effects
The notion of chirality of spin and oscillation of flavor of the defining supersymmetric particles
HELICITY , CHIRALITY AND THE STERILE NEUTRINO
Chirality (physics)
What is helicity?
Chiral spinors and helicity amplitudes | HEP Conference and Awards|#physics #science #space #nasa
Dirac Equation:Chirality and Helicity
Helicity and Chirality
helicity and chirality operator
Chirality, Helicity and Spin
QFT(2022)Lecture 12: Helicity & Chirality of Neutrino (Prof. Binil Aryal, IoST, TU / 7 July 2022...
QFT-13: Helicity & Chirality of Neutrino (Prof. Dr. Binil Aryal, Tribhuvan University, Nepal)
Electron Chirality (extra footage)
Chirality (physics)
Helicity (particle physics)
Chiral Motion of Electrons in a Chern Topological Magnet
Helicity 2 (massive and massless particles)
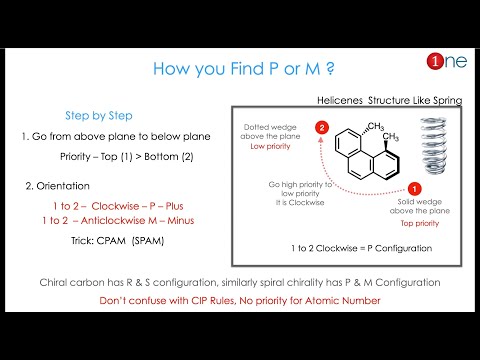
What is P and M Configuration ? & How to Find it ? 🔎🕵| Axial Chirality | Helicity | Stereochemi...
The Chiral Induced Spin Selectivity Effect From The Weismann Institute
Truly chiral phonons in α-HgS
DLS Claudia Felder: Chirality and Topology
Chirality explained under a minute | #chemistry #chemistryfacts #science
Комментарии
 0:06:21
0:06:21
 0:03:10
0:03:10
 0:48:31
0:48:31
 0:02:19
0:02:19
 0:06:09
0:06:09
 0:12:54
0:12:54
 0:03:43
0:03:43
 0:01:00
0:01:00
 0:12:49
0:12:49
 0:07:13
0:07:13
 0:01:01
0:01:01
 0:41:10
0:41:10
 0:54:38
0:54:38
 1:01:25
1:01:25
 0:05:07
0:05:07
 0:15:19
0:15:19
 0:01:58
0:01:58
 0:00:14
0:00:14
 0:08:03
0:08:03
 0:06:01
0:06:01
 0:04:52
0:04:52
 0:00:17
0:00:17
 1:01:42
1:01:42
 0:01:00
0:01:00