filmov
tv
Evaluating (1+i)ⁱ | A Very Complex Number?

Показать описание
If you need to post a picture of your solution or idea:
(1+i)ⁱ = ?
#ChallengingMathProblems #ExponentialEquations #ComplexNumbers
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
⭐ SIMILAR PROBLEMS:
PLAYLISTS 🎵 :
(1+i)ⁱ = ?
#ChallengingMathProblems #ExponentialEquations #ComplexNumbers
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
⭐ SIMILAR PROBLEMS:
PLAYLISTS 🎵 :
Evaluating (1+i)ⁱ | A Very Complex Number?
(1+i)^(1+i) | Complex number in complex power | Math 01/16
How to Evaluate i to a Negative Exponent: Example with i^(-23) #shorts
How to Evaluate the 99th Power of 1-i | #14
What is iⁱ ? Imaginary or Real?
What is the Value of (1-i)^5 | Complex Number | Binomial Expansion
What does an imaginary power mean?
A Quick and Easy Exponential Equation | iˣ = 1
Evaluating A Radical Expression | Two Ways
A Very Interesting Exponential Equation | 1ˣ = -1
Positive Integral Powers of Imaginary Number i (Part 1)
Dividing Complex numbers | How to divide complex numbers | (1+i)/(1-i) | Math 01/02
Find all solutions to (-i) ^ i | An interesting complex analysis problem
Complex Number Trick -2
Evaluating An Algebraic Expression | Two Ways
[Complex Analysis] How to Get the Principle Value of (-i)^i
The value of `[(1+i)^(6) +(1-i) ^(6)]` is-
1+i^2+i^4+i^6+ ….+i^2n is
A Wonderful Math Problem. Ln(1+i)=? Complex Number.
Complex Numbers: Euler's Formula and f(z)=z⁴
COMPLEX NUMBER RAISED TO ANOTHER COMPLEX NUMBER | DE LA CRUZ TUROTIALS
Even teachers get this wrong. Correct answer explained by mathematician
The real and imaginary parts of ln(1+i)^i
Find values of z such that e^z = 1 + i
Комментарии
 0:08:50
0:08:50
 0:02:53
0:02:53
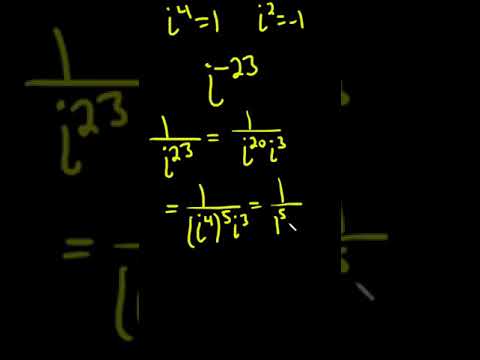 0:01:01
0:01:01
 0:09:40
0:09:40
 0:08:38
0:08:38
 0:05:42
0:05:42
 0:08:15
0:08:15
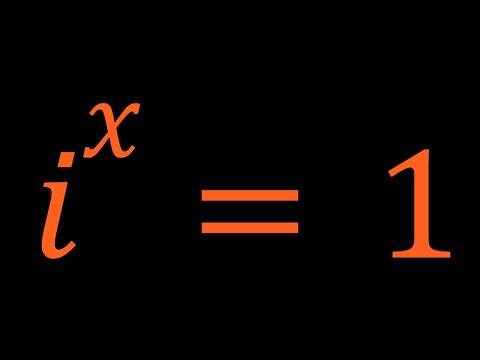 0:09:19
0:09:19
 0:08:38
0:08:38
 0:08:58
0:08:58
 0:00:55
0:00:55
 0:02:28
0:02:28
 0:05:05
0:05:05
 0:01:00
0:01:00
 0:10:01
0:10:01
![[Complex Analysis] How](https://i.ytimg.com/vi/z9MXsDCVVvc/hqdefault.jpg) 0:01:47
0:01:47
 0:03:13
0:03:13
 0:01:49
0:01:49
 0:04:28
0:04:28
 0:10:08
0:10:08
 0:14:58
0:14:58
 0:04:36
0:04:36
 0:08:21
0:08:21
 0:04:06
0:04:06