filmov
tv
Magnetic field of a short wire using the Biot-Savart law with trigonometric substitution.
Показать описание
This time we compute a magnetic field integral using the Biot-Savart law with trigonometric substitution.
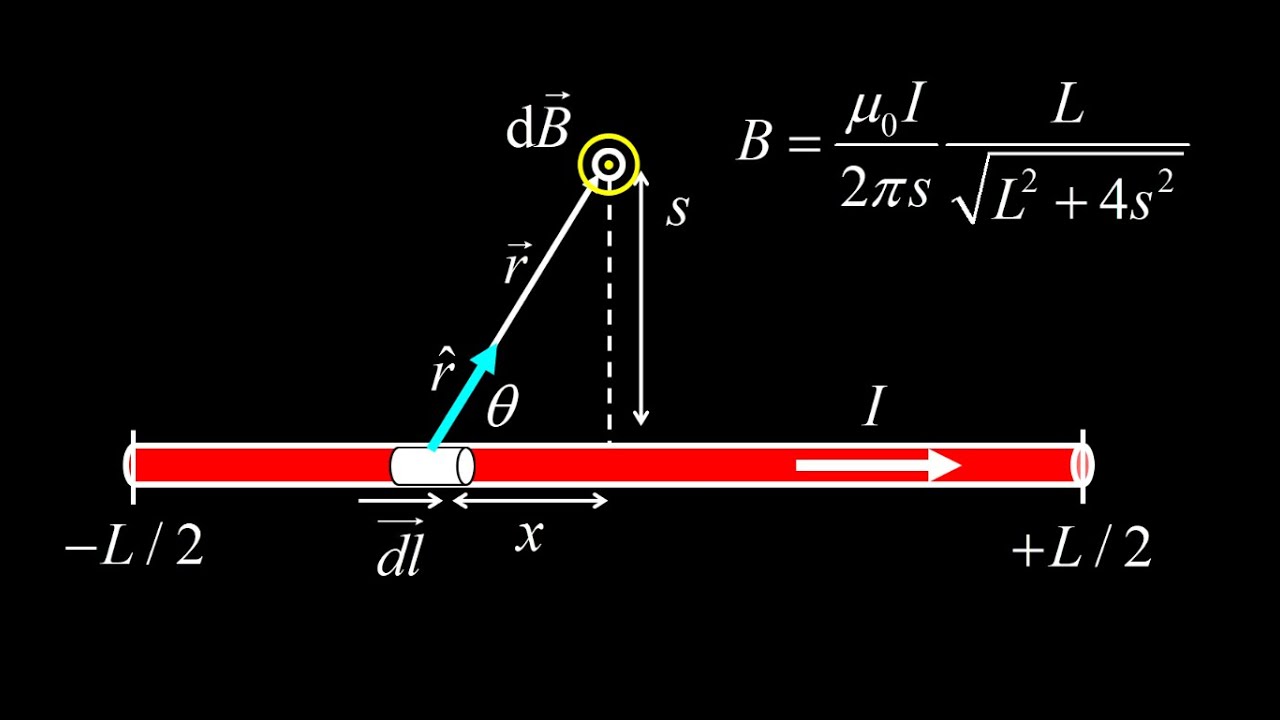
To get the magnetic field of a short wire, we begin with the classic Biot-Savart setup: label a length increment on the wire, dl-vector, draw the position vector r, the unit vector r-hat and label the angle between dl and r-hat. We use a right hand rule to determine the direction of the cross product of dl and r-hat, and this time, we realize every magnetic field contribution points in the same direction (out of the page) so the dB contributions simply add together to get the total magnetic field at a given distance from the short wire.
We write down the Biot-Savart Law and take the magnitude of the magnetic field contribution, since all the contributions point in the same direction anyway and we know we can just sum over the magnitudes to get the final answer. Taking the magnitude of the cross product, we can compute the sine of theta by using right triangle trig to relate the sine function to the opposite side and hypotenuse of a right triangle. We also replace dl with dx, since dl is a small length increment in the x direction, and we express the distance from dl to the observation point by using right triangle trigonometry again to express r in terms of x, the horizontal position from the middle of the short wire to the position of dl. The Biot-Savart integral is now set up entirely in terms of a single integration variable x.
Ignoring the constants, the key feature of this integral is dx/(x^2+s^2)^(3/2), and this integral requires a trigonometric substitution let x=stan(theta). We also transform the differential dx=s*sec^2(theta)d(theta) and we transform the limits of integration to theta-space as well. Computing the integral, we arrive at the solution for the magnetic field on the perpendicular bisector of a short length of current: mu_0*IL/2pis*sqrt(L^2+4s^2).
#physics #magnetism #apphysics
To get the magnetic field of a short wire, we begin with the classic Biot-Savart setup: label a length increment on the wire, dl-vector, draw the position vector r, the unit vector r-hat and label the angle between dl and r-hat. We use a right hand rule to determine the direction of the cross product of dl and r-hat, and this time, we realize every magnetic field contribution points in the same direction (out of the page) so the dB contributions simply add together to get the total magnetic field at a given distance from the short wire.
We write down the Biot-Savart Law and take the magnitude of the magnetic field contribution, since all the contributions point in the same direction anyway and we know we can just sum over the magnitudes to get the final answer. Taking the magnitude of the cross product, we can compute the sine of theta by using right triangle trig to relate the sine function to the opposite side and hypotenuse of a right triangle. We also replace dl with dx, since dl is a small length increment in the x direction, and we express the distance from dl to the observation point by using right triangle trigonometry again to express r in terms of x, the horizontal position from the middle of the short wire to the position of dl. The Biot-Savart integral is now set up entirely in terms of a single integration variable x.
Ignoring the constants, the key feature of this integral is dx/(x^2+s^2)^(3/2), and this integral requires a trigonometric substitution let x=stan(theta). We also transform the differential dx=s*sec^2(theta)d(theta) and we transform the limits of integration to theta-space as well. Computing the integral, we arrive at the solution for the magnetic field on the perpendicular bisector of a short length of current: mu_0*IL/2pis*sqrt(L^2+4s^2).
#physics #magnetism #apphysics
Комментарии
 0:00:31
0:00:31
 0:00:25
0:00:25
 0:00:15
0:00:15
 0:00:58
0:00:58
 0:00:54
0:00:54
 0:14:44
0:14:44
 0:00:17
0:00:17
 0:00:16
0:00:16
 0:44:48
0:44:48
 0:02:01
0:02:01
 0:03:03
0:03:03
 0:20:00
0:20:00
 0:01:01
0:01:01
 0:00:56
0:00:56
 0:00:33
0:00:33
 0:02:21
0:02:21
 0:02:00
0:02:00
 0:02:56
0:02:56
 0:05:31
0:05:31
 0:00:59
0:00:59
 0:00:35
0:00:35
 0:02:01
0:02:01
 0:02:55
0:02:55
 0:00:48
0:00:48