filmov
tv
Why PEMDAS Is A Failure

Показать описание
Though mathematics prides itself on consistency and singular solutions, competing order of operation systems create ambiguity in interpreting identical problems. While acknowledging the historical importance of the conventional order dating back to the 16th century, in this video I discuss an approach for future generations. A healthy skepticism of any singular system encourages deeper understanding, and a broader perspective of mathematics beyond specific methods, highlighting its inherent creativity for diverse applications.
Why PEMDAS Is A Failure
This Made Me Fail 5th Grade Math!
Do you know the Order of Operations? #pemdas #mathtutor #shorts #basicmath
PEMDAS Fail? Simple math problem #math
PEMDAS meaning
PEMDAS Math Problem | Algebra Fundamentals | JusticeTheTutor #math #shorts #maths #mathstricks
PEMDAS | Viral math problem
Viral math problem | PEMDAS rule | Order of operations
American Education Is A Failure 😭 #math #mathematics #bodmas #bidmas #pemdas #arletteamuli #dating...
90% Fail to answer #mathtrick #mathematics #pemdas #calculus
PEMDAS RULE #pemdas
Math Quiz That Will Fail 90% Of People
99% Fail This Math Test #pemdas
Order of Operations: What is 16 ➗4✖️4? #pemdas #bodmas #orderofoperations #math #silentmath
Order of Operation | PEMDAS | BODMAS
Viral Math problem drill-1 | %90 failed! | #mathdrills #pemdas #maths #howto #ahorts #ytshorts
PEMDAS and Integers! #math #maths #mathematics #shorts
What is PEMDAS in Math | Make Math Simple
Why PEMDAS don't work
simple math
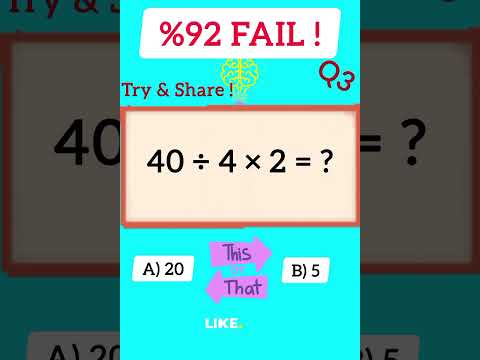
%92 FAIL|Try & Share| 40÷4×2=?| #pemdas #maths #mathstricks #try #share #howtosolve #10k #1kcrea...
Math Quiz #mathpuzzle #pemdas #shorts #mathquiz
Viral math problem#shorts #short #pemdas #mathematics #math #maths #fyp
90% Will fail this😱 #maths #easymathtricks #mathetricks #mathematics #pemdas #operations
Комментарии
 0:10:52
0:10:52
 0:00:15
0:00:15
 0:00:58
0:00:58
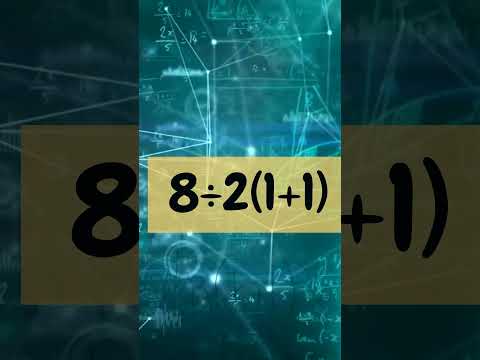 0:00:09
0:00:09
 0:00:15
0:00:15
 0:00:29
0:00:29
 0:00:54
0:00:54
 0:00:09
0:00:09
 0:00:32
0:00:32
 0:01:01
0:01:01
 0:00:10
0:00:10
 0:04:46
0:04:46
 0:00:16
0:00:16
 0:00:29
0:00:29
 0:00:41
0:00:41
 0:00:08
0:00:08
 0:00:47
0:00:47
 0:00:19
0:00:19
 0:01:56
0:01:56
 0:00:12
0:00:12
 0:00:05
0:00:05
 0:00:11
0:00:11
 0:00:29
0:00:29
 0:00:49
0:00:49