filmov
tv
Group Theory: Proof of the Formula for the Inverse of a Product
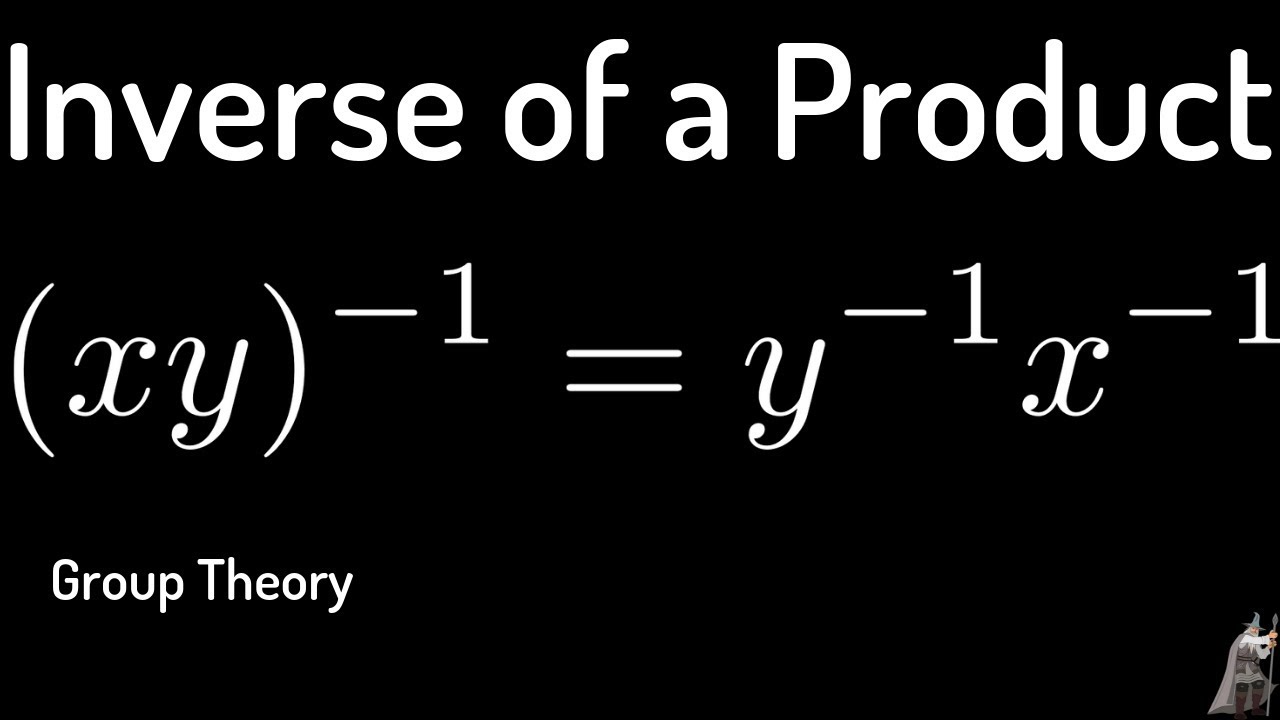
Показать описание
Group Theory: Proof of the Formula for the Inverse of a Product.
Given x, y in G, we prove carefully that (xy)^(-1) = y^(-1)x^(-1).
Given x, y in G, we prove carefully that (xy)^(-1) = y^(-1)x^(-1).
Group theory, abstraction, and the 196,883-dimensional monster
Group Theory Proof: If g^n = e then the order of g divides n
Group Theory: Proof of the Formula for the Inverse of a Product
A Natural Proof of the First Isomorphism Theorem (Group Theory)
Proof in Group Theory Example 1
Group Theory Proof: The order of x is the order of x inverse
Researchers Use Group Theory to Speed Up Algorithms — Introduction to Groups
Cosets and Lagrange’s Theorem - The Size of Subgroups (Abstract Algebra)
Hilbert's Fourteenth Problem
Groups - Showing G is a group - Part 1
Proof: Identity Element of a Group is Unique | Abstract Algebra
Proof: Group Element is the Inverse of its Inverse | Abstract Algebra
Proof & Example: Orbit-Stabilizer Theorem - Group Theory
Proof: Cancellation Law for Groups | Abstract Algebra
A Simple Group Element Inverse Proof | Abstract Algebra
Cosets in Group Theory | Abstract Algebra
Group Theory Proof: The Equation ax = b has a Unique Solution
Group theory 14: Sylow theorems
Isomorphic Groups and Isomorphisms in Group Theory | Abstract Algebra
Proof that inverses in a group are unique
Proof that the identity element of a group is unique
All About Subgroups | Abstract Algebra
Summary: an example covering ALL group theory concepts!! | Essence of Group Theory
Visual Group Theory, Lecture 5.6: The Sylow theorems
Комментарии
 0:21:58
0:21:58
 0:04:05
0:04:05
 0:05:41
0:05:41
 0:13:08
0:13:08
 0:04:37
0:04:37
 0:04:09
0:04:09
 0:31:13
0:31:13
 0:09:19
0:09:19
 1:10:40
1:10:40
 0:05:35
0:05:35
 0:02:42
0:02:42
 0:03:15
0:03:15
 0:17:18
0:17:18
 0:05:47
0:05:47
 0:05:25
0:05:25
 0:15:26
0:15:26
 0:09:27
0:09:27
 0:19:44
0:19:44
 0:13:58
0:13:58
 0:03:00
0:03:00
 0:01:49
0:01:49
 0:15:51
0:15:51
 0:11:27
0:11:27
 0:48:37
0:48:37