filmov
tv
Stable and Unstable Systems (Solved Problems) | Part 1

Показать описание
Signal and System: Solved Questions on Stable and Unstable Systems
Topics Discussed:
1. Examples of stable and unstable systems.
2. Homework problem on stable and unstable systems.
Music:
Axol x Alex Skrindo - You [NCS Release]
#SignalAndSystemByNeso #Signal&System #StableSystem #UnstableSystem #BIBO
Topics Discussed:
1. Examples of stable and unstable systems.
2. Homework problem on stable and unstable systems.
Music:
Axol x Alex Skrindo - You [NCS Release]
#SignalAndSystemByNeso #Signal&System #StableSystem #UnstableSystem #BIBO
Stable and Unstable Systems (Solved Problems) | Part 1
Stable and Unstable Systems
Stable and Unstable Systems (Solved Problems) | Part 2
Stable vs Unstable Systems
Stable and Unstable Systems (Solved Problems)
Stable & Unstable Systems | Digital Signal Processing
Signals & Systems - Stable & Unstable Systems - working examples -1 - UNIT III
Signals & Systems - Stable & Unstable System
Stable & Unstable Systems |Solved problems| (LEC 22)
Stable and Unstable Systems(solved problems )
stable and unstable systems - systems classification - signals and systems
Signals & Systems - Stable & Unstable systems - working examples - 2 - UNIT III
Stable and Unstable Systems, BIBO, bounded input bounded output, exercises, problems, DSP, signal
Signals & System Lect 15 | Stable & Unstable Systems | Solved examples
STABLE and UNSTABLE systems| EXAMPLES
signals and systems- stable and unstable systems |explained with examples
Discrete time stable and unstable systems solved problems |Part 1
EC8352 SIGNALS AND SYSTEMS EXAMPLE PROBLEMS STABLE AND UNSTABLE SYSTEMS CONTINUOUS
EC8352 SIGNALS AND SYSTEMS EXAMPLE PROBLEMS STABLE AND UNSTABLE SYSTEMS DISCRETE
Stable and Unstable Systems Explained: Classification and Examples
Crucial Concepts: Stable And Unstable System For GATE Signals And Systems
Signals & Systems - Stable and Unstable systems - Definition - UNIT III
signals and systems-Discrete time-stable and unstable systems solved problems |part 3
25.2 Stable and Unstable Equilibrium Points
Комментарии
 0:09:50
0:09:50
 0:09:40
0:09:40
 0:06:58
0:06:58
 0:05:06
0:05:06
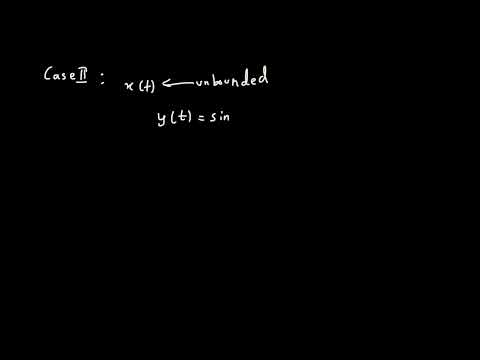 0:07:40
0:07:40
 0:09:03
0:09:03
 0:11:26
0:11:26
 0:09:46
0:09:46
 0:04:59
0:04:59
 0:08:32
0:08:32
 0:06:24
0:06:24
 0:13:09
0:13:09
 0:11:13
0:11:13
 0:19:59
0:19:59
 0:07:52
0:07:52
 0:14:29
0:14:29
 0:11:24
0:11:24
 0:06:19
0:06:19
 0:07:47
0:07:47
 0:07:28
0:07:28
 0:16:59
0:16:59
 0:09:47
0:09:47
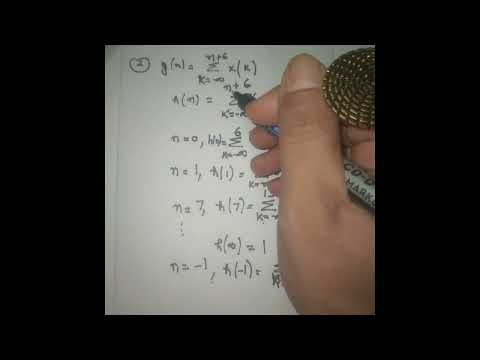 0:18:57
0:18:57
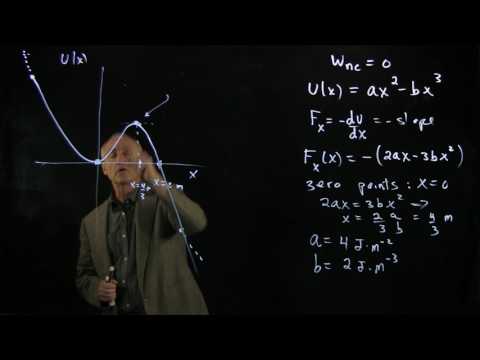 0:07:22
0:07:22