Memory Lane: Vertical and Horizontal, Parallel and Perpendicular

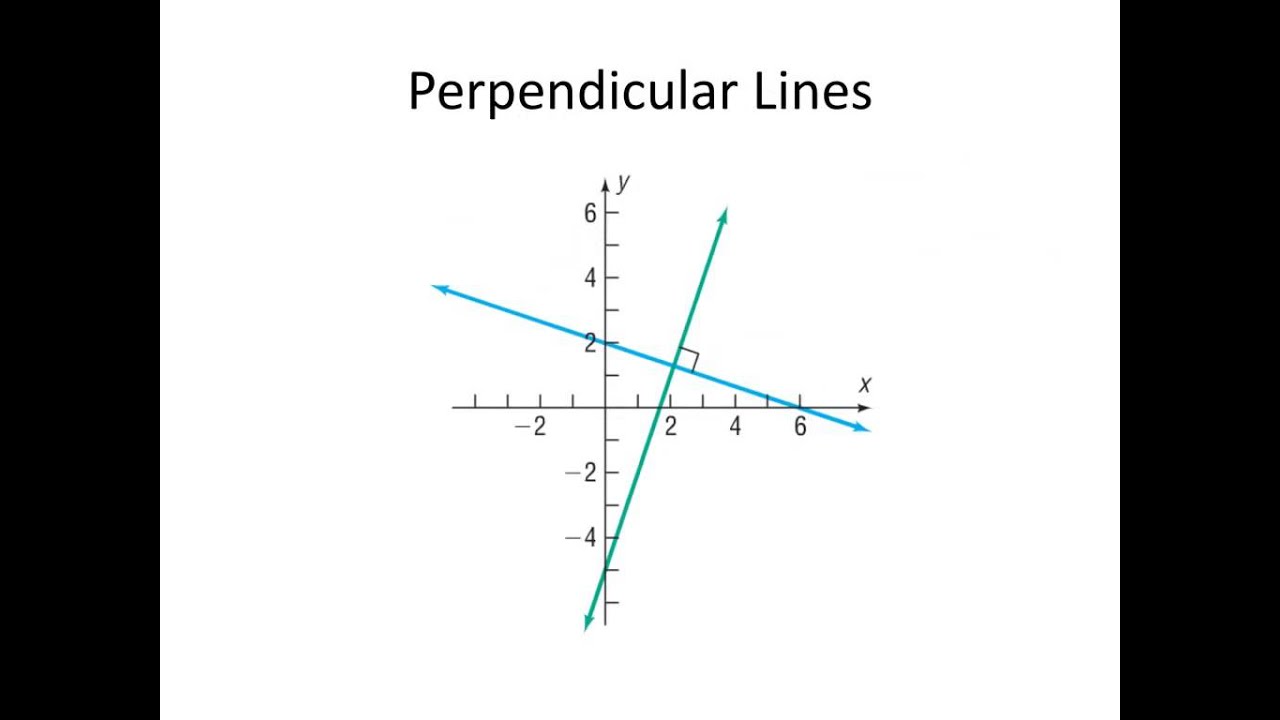
In this video, we look at the equations of vertical and horizontal lines, as well as how to identify when two lines are parallel or perpendicular.

[MikeGreenwood]

Too confusing for me.
But on closer viewing I saw the information is wrong. Or is it wrong? So need to verify. It may just be me who can not follow some point the narrator tries to make about perpendicular.
The video narrator says: if the slopes are negative reciprocals the lines are perpendicular. But the blue triangle is not a reciprocal of the red triangle. Maybe I am confused because his numbers are wrong. The diagram shows a right angle on the blue lines but they meet the X and Y line at different numbers (-4.8 and +6). So numerically the lines can not be a 90° right angle. Or not reciprocal. He is calling his 'red line rise a slope rather than a vertical parallel line parallel to the Y-line. So is it a slope? If it is rising or falling numerically, that would depend on the point of view (POW), IE depending on if the viewer views upwards or downwards.
He said: 'what we see (or say) here is that the slopes are negative reciprocals of each other' (4:49). But the length of the blue and red slopes are diffent lengths. So if they are different lengths (Blue = 4 units, Red =1.5 units (about)). So if you flip those numbers or slopes you do not get a reciprocal. 1.5 does not flip to 4. Except if you flip using a mirror and view them at an angle. Then perpendicular lines could appear different lengths. But that would still not ge perpendicular as one has obscured the image.

It maybe that the principal of the lines and angles are correct but they have been placed in or on a numerically XY grid using numbers. So the numbers do not reciprocate. Therefore the triangles are not reciprocal. But had the two lines and triangles been drawn free standing with out graph, grid or numbers, other than relevant triangle line lengths and angles. Then I think it would be less confusing or clearly presentable. As then the viewer could clearly see the blue triangle if identical to the red triangle in size can be mapped precisely on to the red triangle. Therefor they are reciprocal.