filmov
tv
Hilbert series

Показать описание
Hilbert series (also called Poincare series) are important tools for studying algebra. They give a measure of size for certain vector spaces which have extra structure called a grading. In this video, we introduce the notion of graded vector spaces and their Hilbert series. We show how to compute this Hilbert series for polynomial rings with generators which are not necessarily in degree one. We also look at the ring of symmetric polynomials. We look at some basic properties of HIlbert series such as additivity and shifting which allows us to compute many Hilbert series. As an application, we look at the ordinary double point and show how Hilbert series can be used to identify its coordinate ring as a quotient of a polynomial ring.
Hilbert series
The supersymmetric space of vacua through Hilbert Series
Hilbert Series and Other Advanced Techniques for EFTs by Joydeep Chakraborty
mod10lec49 - Hilbert series - Part 1
Oussama Hamza - Hilbert series and mild groups
mod10lec50 - Hilbert Series - Part 2
Hilbert Series | Regular Sequence | Betti Numbers | Gröbner Basis | Maximal Ideals | Spectrum
Stefano Cremonesi - 3D supersymmetric gauge theories and Hilbert series
Computer Graphics Hilbert Curve SPPU Practical S.E. Engineering in Turbo C#sppu #cg#computergraphics
Graded Rings | Polynomial Rings over a Field | Hilbert Series
HEFT 2021 | Developing the Hilbert series in EFT | Tom Melia
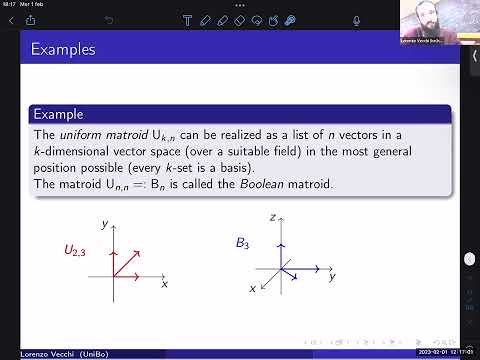
GOCC 2/1/2023 'Hilbert Series of Matroids'
Hilbert Syzygies Theorem
definicoes espaco hilbert series
SunLumin-Architecture Lighting Lens-Hilbert Series
What's a Hilbert space? A visual introduction
Hilbert series and other advanced techniques for EFTs (Lecture 2) by Joydeep Chakrabortty
Hilbert Polynomials for Divisors - part 01
Hilbert said to Einstein:physics is far too complicated to be left to physicists
Commutative algebra 54: Hilbert polynomials
Vecchi: Hilbert-Poincare Series of Matroid Chow Rings and Intersection Cohomology - FPSAC 2023 Davis
How An Infinite Hotel Ran Out Of Room
Hilbert Series and Other Advanced Techniques for EFTs - (Lecture 3) Joydeep Chakraborty
Inner Products in Hilbert Space
Комментарии
 0:41:36
0:41:36
 0:09:55
0:09:55
 1:06:20
1:06:20
 0:35:46
0:35:46
 0:44:14
0:44:14
 0:28:31
0:28:31
 2:06:31
2:06:31
 0:29:49
0:29:49
 0:05:07
0:05:07
 2:08:27
2:08:27
 0:29:19
0:29:19
 1:02:06
1:02:06
 0:16:31
0:16:31
 0:12:18
0:12:18
 0:00:20
0:00:20
 0:06:10
0:06:10
 1:03:24
1:03:24
 0:14:56
0:14:56
 0:01:03
0:01:03
 0:21:53
0:21:53
 0:26:06
0:26:06
 0:06:07
0:06:07
 1:10:22
1:10:22
 0:08:41
0:08:41