filmov
tv
Comment calculer le quartile d une série statistique

Показать описание
comment calculer le quartile d une série statistique
Dans ce tuto le Papillon matheux on va découvrir comment calculer le quartile d une série statistique étape par étape et pour éclaircir davantage cette leçon on finira à donner des exemples sur comment calculer le quartile.
- Le premier quartile (noté Q1) est la valeur d'une série qui est supérieure ou égale à au moins 25 % des données de la série ordonnée de valeurs statistiques.
Appelons N le nombre des valeurs d'une série, et calculons 0,25*N = N/4.
Lorsque N/4 est entier, la valeur représentant le premier quartile est la 0,25e valeur.
Lorsque N/4 est un décimal non entier, on l'arrondit à l'entier supérieur p et alors la valeur représentant le premier quartile est la p-ième valeur.
Exemple 1: Dans la série 10; 25; 30; 40; 41; 42; 50; 55; 70; 101; 110; 111, le premier quartile est 30. En effet, il y a 12 nombres dans cette série, et 12/4=3 . Le premier quartile est donc la 3e valeur, soit 30.
Exemple 2 : si N/4=4,25, Q1 est égale à la cinquième valeur (attention, ce n'est pas 5).
- Le troisième quartile (noté Q3) est la valeur d'une série qui est supérieure ou égale à au moins 75 % des données de la série ordonnée de valeurs statistiques.
Lorsque 3N/4 est entier, la valeur représentant le premier quartile est la 0,75e valeur.
Lorsque 3N/4 est un décimal non entier, on l'arrondit à l'entier supérieur p et alors la valeur représentant le troisième quartile est la p-ième valeur.
Exemple : Dans la série: 10; 25; 30; 40; 41; 42; 50; 55; 70; 101; 110; 111, le troisième quartile est 70. En effet, il y a 12 nombres dans cette série, et 0,75*12 = 9. Le troisième quartile est donc la 9e valeur, soit 70.
Exemple 2 : si 3N/4=0,75N=15,25, Q3 est égale à la seizième valeur (attention, ce n'est pas 16).
- L'écart interquartile représente la différence entre Q3 et Q1.
Exemple : Dans la série 10; 25; 30; 40; 41; 42; 50; 55; 70; 101; 110; 111, l'écart interquartile est 40. En effet, Q3 valant 70 et Q1 valant 30, il suffit de calculer 70-30.
J'espère que cette leçon était très bénéfique pour vous et que vous avez appris comment calculer les quartiles d une série statistique.
N'hésitez pas à poser vos questions dans les commentaires sur le sujet " comment calculer un quartile d une serie statistique " ou un autre sujet mathématique. J’essayerai de répondre au maximum à vos questions
Je resterai à votre disposition si vous avez des remarques ou des propositions pour améliorer cette leçon intituler " comment trouver le quartile "
Sujet similaires à " comment calculer le quartile "
Liens de vidéos à ajouter
Dans ce tuto le Papillon matheux on va découvrir comment calculer le quartile d une série statistique étape par étape et pour éclaircir davantage cette leçon on finira à donner des exemples sur comment calculer le quartile.
- Le premier quartile (noté Q1) est la valeur d'une série qui est supérieure ou égale à au moins 25 % des données de la série ordonnée de valeurs statistiques.
Appelons N le nombre des valeurs d'une série, et calculons 0,25*N = N/4.
Lorsque N/4 est entier, la valeur représentant le premier quartile est la 0,25e valeur.
Lorsque N/4 est un décimal non entier, on l'arrondit à l'entier supérieur p et alors la valeur représentant le premier quartile est la p-ième valeur.
Exemple 1: Dans la série 10; 25; 30; 40; 41; 42; 50; 55; 70; 101; 110; 111, le premier quartile est 30. En effet, il y a 12 nombres dans cette série, et 12/4=3 . Le premier quartile est donc la 3e valeur, soit 30.
Exemple 2 : si N/4=4,25, Q1 est égale à la cinquième valeur (attention, ce n'est pas 5).
- Le troisième quartile (noté Q3) est la valeur d'une série qui est supérieure ou égale à au moins 75 % des données de la série ordonnée de valeurs statistiques.
Lorsque 3N/4 est entier, la valeur représentant le premier quartile est la 0,75e valeur.
Lorsque 3N/4 est un décimal non entier, on l'arrondit à l'entier supérieur p et alors la valeur représentant le troisième quartile est la p-ième valeur.
Exemple : Dans la série: 10; 25; 30; 40; 41; 42; 50; 55; 70; 101; 110; 111, le troisième quartile est 70. En effet, il y a 12 nombres dans cette série, et 0,75*12 = 9. Le troisième quartile est donc la 9e valeur, soit 70.
Exemple 2 : si 3N/4=0,75N=15,25, Q3 est égale à la seizième valeur (attention, ce n'est pas 16).
- L'écart interquartile représente la différence entre Q3 et Q1.
Exemple : Dans la série 10; 25; 30; 40; 41; 42; 50; 55; 70; 101; 110; 111, l'écart interquartile est 40. En effet, Q3 valant 70 et Q1 valant 30, il suffit de calculer 70-30.
J'espère que cette leçon était très bénéfique pour vous et que vous avez appris comment calculer les quartiles d une série statistique.
N'hésitez pas à poser vos questions dans les commentaires sur le sujet " comment calculer un quartile d une serie statistique " ou un autre sujet mathématique. J’essayerai de répondre au maximum à vos questions
Je resterai à votre disposition si vous avez des remarques ou des propositions pour améliorer cette leçon intituler " comment trouver le quartile "
Sujet similaires à " comment calculer le quartile "
Liens de vidéos à ajouter
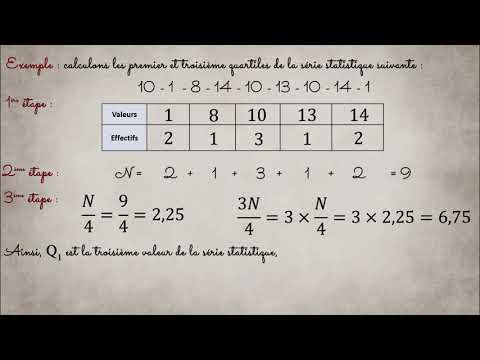 0:09:52
0:09:52
 0:05:10
0:05:10
 0:08:39
0:08:39
 0:08:36
0:08:36
 0:01:38
0:01:38
 0:05:29
0:05:29
 0:01:30
0:01:30
 0:06:22
0:06:22
 0:06:25
0:06:25
 0:03:45
0:03:45
 0:02:02
0:02:02
 0:01:25
0:01:25
 0:12:04
0:12:04
 0:11:21
0:11:21
 0:07:00
0:07:00
 0:06:13
0:06:13
 0:02:51
0:02:51
 0:04:48
0:04:48
 0:11:58
0:11:58
 0:15:47
0:15:47
 0:09:19
0:09:19
 0:11:52
0:11:52
 0:11:02
0:11:02
 0:11:08
0:11:08