filmov
tv
L3. Prefix, Infix, and Postfix Conversion | Stack and Queue Playlist

Показать описание
L3. Prefix, Infix, and Postfix Conversion | Stack and Queue Playlist
Infix to Postfix conversions example | Data Structures | Lec-15 | Bhanu Priya
3.6 Infix to Postfix using Stack | Data Structures Tutorials
Evaluation of Postfix Expression | Examples | Data Structures | Lec-20 | Bhanu Priya
PDS: L21: Prefix Evaluation and Infix to Postfix
TREE |Binary Search Tree |Traversal Algorithms | Infix, Prefix, and Postfix Notation | L4
3.10 Postfix Expression Evaluation using Stack | Data Structures and Algorithms
Infix Evaluation | Stacks and Queues | In English | Java | Video_8
Infix to Postfix conversion using stack | Stack | Data Structures | CSE
Postfix Evaluation and Conversion | Stacks and Queues | In English | Java | Video_10
infix to prefix conversion
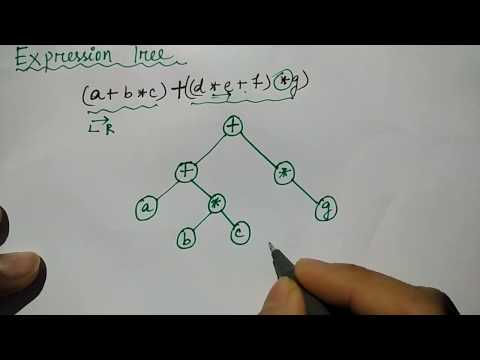
expression tree in data structure | infix expression | HINDI | Niharika Panda
Prefix Evaluation and Conversion | Stacks and Queues | In English | Java | Video_11
Stack Notification - Introduction and Infix to Postfix Conversion (Numerical Part 1)
Postfix notation Meaning
Infix Evaluation | Module : Stacks and Queues | In Hindi | C++ | Video_8
Prefix Evaluation and Conversion | Module : Basics Data Structures | In English | Python | Video_11
Lec 11 Postfix and Prefix Evaluation || GATE Insights Version: CSE
#3. Algorithm to evaluate postfix expression (AKTU 2023 QUESTION) //@brevilearning
class 12 -Data structure-II prefix/postfix to infix conversion using stack.
Stack Notification - Introduction and Infix to Postfix Conversion (Numerical Part 2)
Infix Evaluation | Module : Basics Data Structures | In Hindi | Python | Video_8
Postfix Evaluation and Conversion | Module : Basics Data Structures | In English | Python | Video_10
81. Evaluation of Postfix (Hindi)
Комментарии
 0:50:47
0:50:47
 0:12:14
0:12:14
 0:20:10
0:20:10
 0:04:23
0:04:23
 0:47:09
0:47:09
 0:55:46
0:55:46
 0:11:02
0:11:02
 0:25:45
0:25:45
 0:18:31
0:18:31
 0:20:35
0:20:35
 0:09:02
0:09:02
 0:04:56
0:04:56
 0:16:31
0:16:31
 0:12:03
0:12:03
 0:00:28
0:00:28
 0:18:01
0:18:01
 0:15:27
0:15:27
 0:10:47
0:10:47
 0:05:04
0:05:04
 0:09:48
0:09:48
 0:13:03
0:13:03
 0:21:23
0:21:23
 0:13:36
0:13:36
 0:10:26
0:10:26