filmov
tv
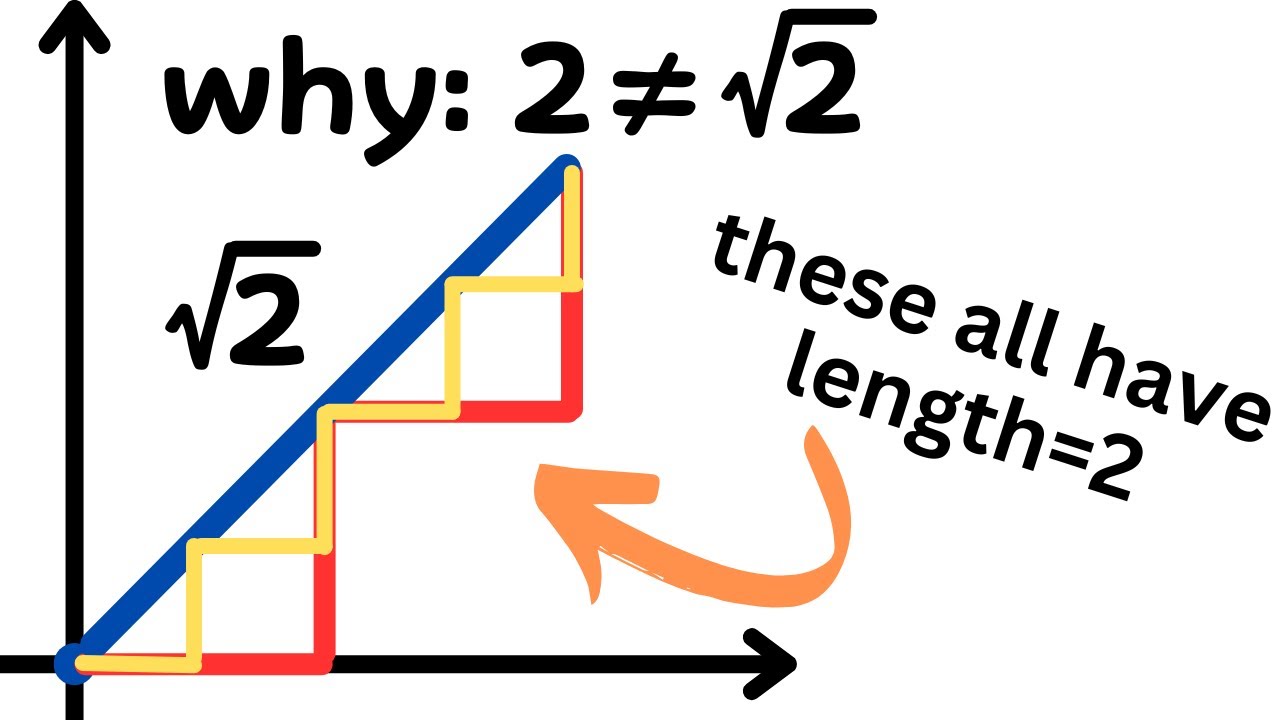
A classic puzzle
Показать описание
🌟Support the channel🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
This is a classic topological space escape.#puzzle#iq#iqtest
This is a classic reverse thinking puzzle#puzzle#iq#iqtest
Problem of the Two Doors: Classic Logic Puzzle
This is a classic reverse thinking topology puzzle#puzzle#iq#iqtest
The Wason Selection Task || Classic Puzzle #03
This is a classic topological metal puzzle#puzzle#iq#iqtest
Try to put this square in the frame | how is it possible?
A classic topological disentanglement puzzle: The Mouse Ladder#puzzle#iq#iqtest
Only One Can Ride the Boat... Can You Solve This Classic Puzzle?
A classic topology puzzle, can you separate these two nails?#iqtest #iq #puzzle
How To Solve the 6 Piece Wooden cross Puzzle
This is a classic topological knot escape puzzle#puzzle#iq#iqtest
This is a classic reverse-thinking topology puzzle#puzzle#iq#iqtest
This is a classic puzzle from an intelligence test#puzzle#iq#iqtest
Solving A Classic Google Interview Logic Puzzle
This is a typical brain teaser test#puzzle#iq#iqtest
ROKR Classic Printing Press Mechanical 3D Wooden Puzzle LK602
The Classic Box - A Lego Puzzle Trick Box [Solve]
A classic puzzle from 1940:How can these four T-shaped wooden blocks all fit into a circle?
Horse puzzle |#youtubeshorts
One Simple Trick Turns this Puzzle into a Classic Children's Game
A Classic Math Puzzle That Stumps Everyone! 🤯 #puzzle
Hogtie - a classic puzzle unique adventure game combines Sokoban style mechanics
The classic Tower of Hanoi puzzle from 1883#puzzle#iq#iqtest
Комментарии
 0:00:57
0:00:57
 0:00:49
0:00:49
 0:03:25
0:03:25
 0:00:58
0:00:58
 0:07:52
0:07:52
 0:00:55
0:00:55
 0:10:04
0:10:04
 0:00:58
0:00:58
 0:00:56
0:00:56
 0:01:00
0:01:00
 0:02:15
0:02:15
 0:01:00
0:01:00
 0:01:00
0:01:00
 0:00:59
0:00:59
 0:09:03
0:09:03
 0:00:49
0:00:49
 0:00:34
0:00:34
 0:02:09
0:02:09
 0:00:30
0:00:30
 0:00:23
0:00:23
 0:06:40
0:06:40
 0:00:31
0:00:31
 0:00:47
0:00:47
 0:01:00
0:01:00