filmov
tv
Special Relativity and Hyperbolic Numbers

Показать описание
A brief introduction to Hyperbolic Numbers and their application to SR.
// Patreon
--- Music ---
Happy - LoFi Ocean
// Patreon
--- Music ---
Happy - LoFi Ocean
Special Relativity and Hyperbolic Numbers
Relativity 104e: Special Relativity - Spacetime Interval and Minkowski Metric
Relativity 105a: Acceleration - Hyperbolic Motion and Rindler Horizon
Lorentz Transformations | Special Relativity Ch. 3
Minkowski SPACETIME, Hyperbolic Geometry & Lorentz Transformations | STR
The applications of hyperbolic trig | Why do we even care about these things?
How One Line in the Oldest Math Text Hinted at Hidden Universes
Non-Euclidean Geometry Explained - Hyperbolica Devlog #1
Acceleration in Special Relativity
Hyperbolic Motion in Special Relativity - Animated Spacetime Diagram
The Lorentz Transformations - Intuitive Explanation
Albert Einstein doing physics | very rare video footage #shorts
Split Complex Numbers and the Lorentz Boost
The secrets of Einstein's unknown equation – with Sean Carroll
Relativity 101b: Introduction to Special Relativity
Spacetime Intervals: Not EVERYTHING is Relative | Special Relativity Ch. 7
A Swift Introduction to Spacetime Algebra
How Does DRAGON BALL Z's Time Chamber Work? (Because Science w/ Kyle Hill)
Length Contraction is NOT an Illusion!
Hyperbolic Geometry | Relativity 11
Premise of Special Relativity | General Relativity
Hyperbolic Geometry is Projective Relativistic Geometry
Special Relativity: Four-Vectors and Covariance
Special Relativity and your FUTURE. #Shorts
Комментарии
 0:06:41
0:06:41
 0:34:19
0:34:19
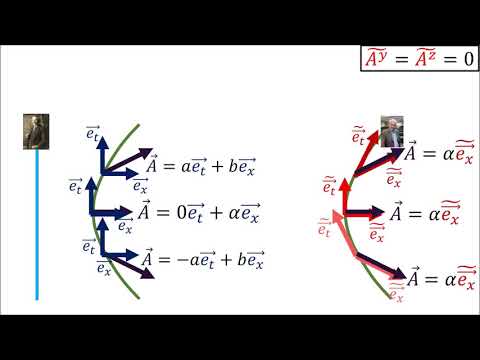 0:31:37
0:31:37
 0:12:18
0:12:18
 1:00:15
1:00:15
 0:14:45
0:14:45
 0:31:12
0:31:12
 0:10:54
0:10:54
 0:58:35
0:58:35
 0:01:07
0:01:07
 0:16:56
0:16:56
 0:00:13
0:00:13
 0:29:14
0:29:14
 0:53:59
0:53:59
 0:15:20
0:15:20
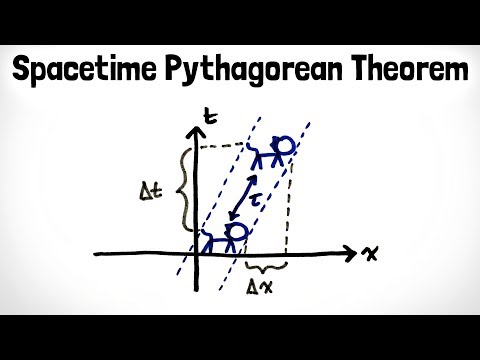 0:07:26
0:07:26
 0:38:59
0:38:59
 0:05:08
0:05:08
 0:10:19
0:10:19
 0:12:08
0:12:08
 0:32:16
0:32:16
 0:51:17
0:51:17
 0:37:23
0:37:23
 0:01:00
0:01:00