filmov
tv
Addition Formulae using Matrices?! - Complex Numbers, but Different [ Bonus 1 ]

Показать описание
Help me create more free content! =)
Todaay my good friend Sam from Whatthehectogon wants to show youi the art of deriving trigonometric addition formulas for the sin and cosine, using complex numebrs in matrix form! =) Don't forget subscribing to his channel :)
--------------------------------------------------------------------------------
Wanna send me some stuff? lel:
Postfach 60 06 03
14406 Potsdam
Brandenburg
Germany
--------------------------------------------------------------------------------
Addition Formulae using Matrices?! - Complex Numbers, but Different [ Bonus 1 ]
Adding and Subtracting Matrices
Addition of Matrices Class 9
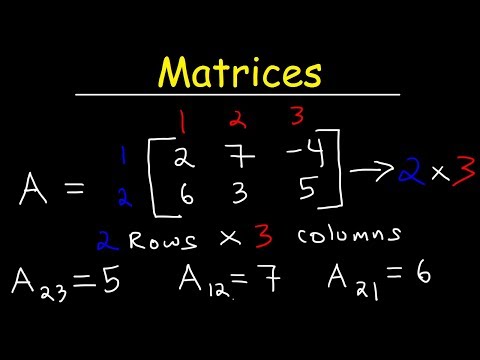
Intro to Matrices
Matrix addition and subtraction | Matrices | Precalculus | Khan Academy
Solving Matrix Equations
Part 1, Solving Using Matrices and Cramer's Rule
How To Perform Elementary Row Operations Using Matrices
Matrix Multiplication, Transposition, Matrix Representation of a Vector, Vector Rotation
Types of Matrices and Matrix Addition
Simultaneous Equations Matrix Method : ExamSolutions
How to solve System of linear Equations using Matrices
Part 2, Solving Using Matrices and Cramer's Rule, 3 Variables with 3 Equations
Matrix multiplication as composition | Chapter 4, Essence of linear algebra
Linear transformations and matrices | Chapter 3, Essence of linear algebra
Understanding Matrices and Matrix Notation
Solve by Matrix Method | Matrix Method | Matrices | MindYourChoices @mindyourchoices
Matrices - System of Linear Equations (Part 1) | Don't Memorise
Solving simultaneous equations using matrices
Linear Algebra - Matrix Operations
FORM 3 MATHS (Solving Simultaneous Equations Using Matrices)
Gaussian Elimination & Row Echelon Form
Determinant of a Matrix Class 9
Functions of EXCEL for Matrix Operations | Matrix Addition, Multiplication, Inverse using Excel
Комментарии
 0:19:45
0:19:45
 0:06:12
0:06:12
 0:00:24
0:00:24
 0:11:23
0:11:23
 0:05:35
0:05:35
 0:06:31
0:06:31
 0:04:11
0:04:11
 0:08:48
0:08:48
 0:25:01
0:25:01
 0:06:46
0:06:46
 0:09:23
0:09:23
 0:08:36
0:08:36
 0:08:51
0:08:51
 0:10:04
0:10:04
 0:10:59
0:10:59
 0:05:26
0:05:26
 0:05:23
0:05:23
 0:04:04
0:04:04
 0:04:10
0:04:10
 0:07:08
0:07:08
 0:16:07
0:16:07
 0:18:40
0:18:40
 0:00:18
0:00:18
 0:14:36
0:14:36