filmov
tv
Calculus 3: Triple Integrals (6 of 25) Finding the Volume of a Cone: Part 1: Spherical

Показать описание
In this video I will find volume of a cone using triple integrals in the spherical coordinate system.
Next video in this series can be seen at:
Calculus 3 Lecture 14.6: How to Solve TRIPLE INTEGRALS (Along with Center of Mass and Volume)
Calculus 3: Triple Integrals (6 of 25) Finding the Volume of a Cone: Part 1: Spherical
Triple Integrals - Calculus 3
Calculus 3: Triple Integrals (Video #23) | Math with Professor V
Calculus 3: Ch 13.1 Triple Integrals (6 of TBD) Triple Inttegral: Example 2
Calc III: Triple Integral in Spherical Coordinates example 5/6
Calc III: Triple Integral in Spherical Coordinates example 3/6
Triple Integrals Practice Problems
Double And Triple Integrals |01| BSc 1st Semester Maths 2nd Book Integral Calculus Unit 2 Chapter 6
Calc III: Triple Integral in Spherical Coordinates example 4/6
Triple Integrals in Cartesian Coordinates | Volume between Surfaces
15.6: Triple Integrals
Triple integral in six different ways - reversing the order of integration
Expressing a triple iterated integral 6 ways (KristaKingMath)
Double and Triple Integrals
Calculus - How to find the bounds of a triple integral
14.06.06 Finding Limits for Triple Integrals
Triple Integrals in Spherical Coordinates
ALL of calculus 3 in 8 minutes.
Calc III: Triple Integral in Spherical Coordinates example 6/6
Triple Integrals Part 2: Volume of a Tetrahedron computed 2 ways
How to change the order of a triple integral
Calculus III 15 6 Triple Integrals
Calc III: Triple Integral in Spherical Coordinates example 1/6
Комментарии
 3:33:32
3:33:32
 0:06:55
0:06:55
 0:10:06
0:10:06
 0:56:38
0:56:38
 0:05:20
0:05:20
 0:07:58
0:07:58
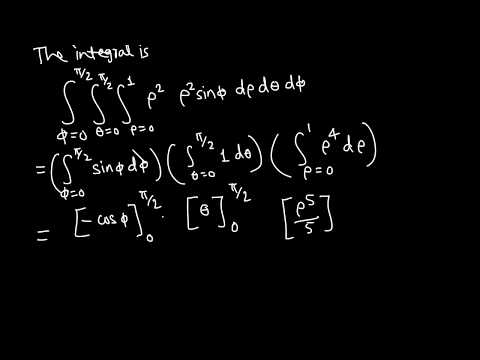 0:04:17
0:04:17
 0:20:34
0:20:34
 0:56:30
0:56:30
 0:03:45
0:03:45
 0:07:13
0:07:13
 0:40:27
0:40:27
 0:25:46
0:25:46
 0:18:15
0:18:15
 0:15:29
0:15:29
 0:04:56
0:04:56
 0:10:40
0:10:40
 0:28:43
0:28:43
 0:08:10
0:08:10
 0:07:40
0:07:40
 0:11:44
0:11:44
 0:09:40
0:09:40
 1:14:17
1:14:17
 0:06:30
0:06:30