Edmentum Integrated Math2 Unit 6 Activity: AA, SAS, and SSS Criteria for Similar Triangles

You will use the GeoGebra geometry tool to investigate how many pairs of corresponding angles in two triangles are enough to prove that the two triangles are similar. Open GeoGebra, and complete each step below. If you need help, follow these instructions for using GeoGebra.

Create a random triangle, ΔABC. Measure and record its angles.

Now you will attempt to copy your original triangle using one of its angles:

Draw a line segment, , of any length anywhere on the coordinate plane, but not on top of ∆ABC.
Choose one of the angles on ∆ABC. From point D, create an angle of the same size as the angle you chose. Then draw a ray from D through the angle. You should now have an angle that is congruent to the angle you chose on ∆ABC.
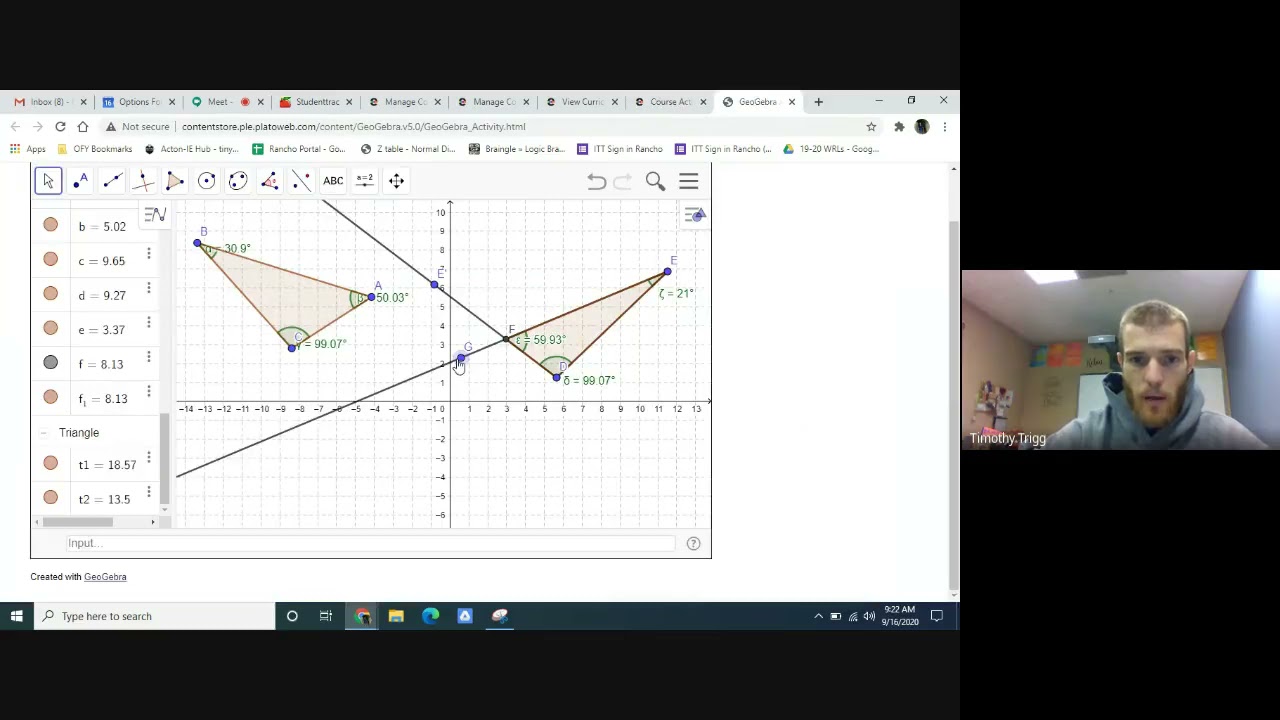
Create a point anywhere outside the mouth, or opening, of the angle you created. The point will initially be named F by the tool, but you should rename it point G. Now draw a ray from E through G such that it intersects the first ray. Your creation should be a closed shape resembling a triangle.
Label the point of intersection of the two rays F, and draw ∆DEF by creating a polygon through points D, E, and F.
Click on point G, and move it around. By moving point G, you can change and , while keeping fixed.
Take a screenshot of your results for one position of G, save it, and insert the image in the space below.

In GeoGebra, label the measures of the three angles on ∆DEF. Then move point G around the coordinate plane to produce triangles with different sets of angles. Record at least five sets of angles as you move G.

By moving point G, how many triangles is it possible to draw, keeping the measure of just one angle constant (in this case, m∠FDE)? In how many instances are all three angle measures of ∆DEF equal to those of the original triangle, ∆ABC?

To decide whether two triangles are similar, is it enough to know that one pair of corresponding angle measures is equal? Use your observations and your understanding of similarity transformations to explain your answer.

As you saw in the previous activity, knowing that one pair of corresponding angle measures in two triangles is equal is not enough to prove that they are similar. Some additional information must be required to prove triangle similarity. Next you’ll investigate whether two pairs of corresponding angles in two triangles having equal angle measures is necessary and sufficient to prove that the triangles are similar. Open GeoGebra again, and complete each step below.

Now you’ll attempt to copy your original triangle using two of its angles:

Choose two of the angles on ∆ABC, and locate the line segment between them. Draw a new line segment, , parallel to the line segment you located on ∆ABC. You can draw of any length and place it anywhere on the coordinate plane, but not on top of ∆ABC.
From points D and E, create an angle of the same size as the angles you chose on ∆ABC. Then draw a ray from D and a ray from E through the angles such that the rays intersect. You should now have two angles that are congruent to the angles you chose on ∆ABC.
Label the point of intersection of the two rays F, and draw ∆DEF by creating a polygon through points D, E, and F.
Take a screenshot of your results, save it, and insert the image in the space below.

How do the angles of ∆DEF compare with those in the original triangle? In particular, compare the angle that you did not set in ∆DEF with the corresponding angle in ∆ABC.

With two of the angles fixed on ∆DEF, what do you notice about the shape of ∆DEF when compared with ∆ABC?

Pick any side of ∆DEF, and find its length. Find the ratio (n) of this side to the corresponding side of ∆ABC.

Dilate ∆ABC about the origin using the scale factor n. Measure and compare the lengths of the sides of the dilated triangle, ∆A'B'C', with those of ∆DEF. Take a screenshot of your dilation, save it, and insert the image below the table.

What can you conclude about ∆A'B'C' and ∆DEF based on their side lengths, angle measures, or both?

Explain why there must be a sequence of rigid transformations that will map ∆A'B'C' exactly onto ∆DEF. Find and perform one such sequence of rigid transformations. Describe the sequence of rigid transformations you performed.

Based on your responses to parts H and I, what can you conclude about ∆ABC and ∆DEF? Explain your answer in terms of similarity transformations.

To decide whether two triangles are similar, is it enough to know that two pairs of corresponding angle measures in the triangles are equal? Use your observations and your understanding of similarity to explain your answer.