Vector addition and basis vectors | Linear algebra makes sense

Vectors may seem very difficult when you're first introduced to them, but I hope this video helps you see they're not that scary! This video will be especially useful for vectors in physics. We'll cover vector addition and what vectors are. This is the start of a whole series of linear algebra, and I will cover vectors, adding vectors physics, the scalar product, matrices, eigenvalues/ eigenvectors and Dirac notation.

DON'T FORGET TO DO YOUR HOMEWORK:

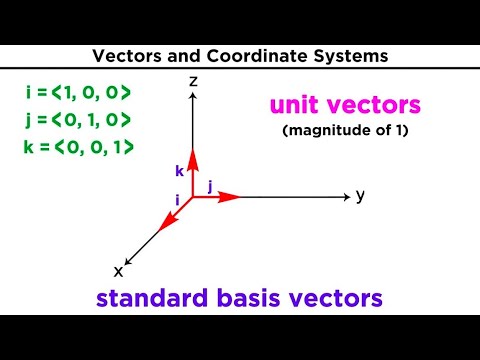
Prove these 2 statements about bases
1. If you have two different bases for the same space, then they must have the same number of basis elements in them. (E.g, there are many different choices of basis for the plane, but no matter what basis you choose, there are only 2 vectors in each basis.)

2. Once you pick a basis (say {v_1, v_2}), there's only one correct way to write another vector as a linear combination of the basis vectors. Eg, say v=a v_1+ b v_2. Then you can't also write v=a' v_1+ b' v_2, where a' and b' are different from a and b.

The multiple choice questions from Brilliant:
Q1. Which of these vectors is redundant (i.e. can be written as a linear combination of the other 2):
i) (1 2 3)
ii) (1 3 5)
iii) (2 5 8)
iv) Each of the above

Q2. Consider the following 3 vector spaces:
A= The vector space spanned by {(1 2)}
B= The vector space spanned by {(1 2), (2 3)}
C= The vector space spanned by {(1 2), (2 4), (3 6)}
Question: which of the following is true?
i) A is a subspace of B, which is a subspace of C
ii) C is a subspace of A, which is a subspace of B
iii) B is a subspace of C, which is a subspace of A
iv) A is a subspace of B and C, which are not subspaces of each other

ANSWERS FOR THE BRILLIANT.ORG QUESTIONS:
*
*
*
*
*
*
*
*
Q1) D
Q2) ii

HINTS FOR PROOF QUESTIONS:
2 is easier, so let's do that first

Hint 2.1 Let's do the case with just 2 basis vectors first. If there are 2 basis vectors v_1 and v_2, the one thing you know about them is that they are not just a multiple of each other (otherwise it wouldn't be a basis). Try and get a contradiction with this fact.

*
*
*

Hint 2.2 Assume v= a v_1+ b v_2 = a' v_1+ b' v_2, but a and a' aren't equal, and b and b' aren't equal.

*
*
*

Hint 2.3 Use the above equation to write a relationship between v_1 and v_2. Oh no, that looks like they are multiples of each other!

*
*
*

Hint 2.4 Now do the case where there are n basis vectors. What you know about them is that you can't write them as linear combinations of the others. Try and get a contradiction with this fact.

*
*
*

Hint 1.1. Imagine you had 3 vectors and they span 2D space. Doesn't that one of them is redundant? The following in this case first:
B1={u_1,u_2}
B2={v_1, v_2,v_3}
Write each u_i in terms of B1.
Remember that there is a redundancy in B2 if you can write c u_1+ d u_2= u_3. So write this, and let's see if we can find a solution for c and d.
Plug in your equations for u_i into c u_1+ d u_2= u_3
You now have a vector on the right hand side in B1 and a vector on the left hand side in B1
Using the result from question 2 (dammit, I really should have swapped the order of these questions), you know that the coefficient in front of v_1 and v_2 must be the same on both sides (since there is only one unique way to write a vector in B1)
So now you have 2 linear equations with 2 unknowns (c and d- everything else is 'known').
Show that they only don't have a solution for c and d if B2 was actually linearly dependent all along. (Yes this will require you to know some linear algebra to do efficiently (although technically possible without)).

*
*
*
When you assume that the two bases can be any size it's most efficient to do this with linear algebra (sorry!!)

*
*
*

Music: Epidemic sound, Summer nights 2

[dancingleaf]

making a poll and stuff is brilliant, it makes it hard to lose concentration because youre doing something and not only listening (did not see that pun until the ad rolled in)

[aniksamiurrahman]

So this enigmatic |v> just means v is a vector!! Curse you Dirac!!!

[eruyommo]

Really. This was more intuitive than my classes of Analytical Geometry and Linear Algebra. Love.

[MirorRflction]

YES! Look forward to the rest of the series! :D The polling thing built into the video was super helpful!

[chicchi]

wish my linear algebra professor taught this as perfect as you did.

[MrGooglevideoviewer]

I like the music you've incorporated in the background, and I appreciate the production effort you're putting in. I've seen a few people comment now that they don't like the music track so I just thought I'd throw this in so that you knew that not everyone thought so. Cheers!

[adityakhanna]

Homework Time!
<note: a1 represents a_1> -I am lazy :P-
First, we start by proving uniqueness of representation. Let the vectors be, *v1*, *v2*, *v3* ... *vN* . Because they are linearly independent,
a1 ⋅ *v1* + a2 ⋅ *v2* ... + aN ⋅ *vN* = 0, only when all of the coefficients are simultaneously zero (this can be seen by taking any one vector to the other side, then dividing by its coefficient and saying that no non-zero solution to that equation exits because linear independence kicks in).
So, once we are given two representations of the same vector, we start be equating both representations, and taking one to the other side resulting in a subtraction
Thus, if a1 ⋅ *v1* + a2 ⋅ *v2* ... + aN ⋅ *vN* and b1 ⋅ *v1* + b2 ⋅ *v2* .+... bN ⋅ *vN* represent the same vector,
then sum[(ai-bi) ⋅ *vi* ] = 0, for all i <= N which means a1 = b1, a2 = b2 and so on.
This proves uniqueness. So, for any system to be a basis, it must have a unique representation for every vector in its span.
This also gives us an easy way, that s, comparing coefficients.

Secondly, we have to prove that for any set to be a basis, the number of vectors should be the same. The following proof technique relies on choosing a vector set and comparing another purported "new basis set" which has one more element than the "chosen one".
This, we will see, contradicts the condition of uniqueness and does not qualify as a basis set due to extra members. This does not in any way tell us the minimum number of vectors required as there is no restriction on the chosen set. But we can remove all those sets whose span is of lesser dimensions than required. Thus, we can choose a set and prove that addition of members does not result in a basis set and then compare the chosen set to a set with one less member. Whenever we reach a point which makes the span dimension lesser than required, we stop.

Here is the proof that addition of members violates uniqueness,
Let the chosen "basis" (lowest) be B = { *v1*, *v2*, ..., *vN* } while the other ""basis"" (heavy airquotes) be
B' = { *u1*, *u2*, ..., *uN*, *u[N+1]* }.
Now, every vector in B' can be written as a linear combination of elements of B.
*u1* = x1 ⋅ *v1* + x2 ⋅ *v2* +... + xN ⋅ *vN*
*u2* = y1 ⋅ *v1* + x=y2 ⋅ *v2* +... + yN ⋅ *vN*
.
.
.
*u[N+1]* = z1 ⋅ *v1* + z2 ⋅ *v2* +... + zN ⋅ *vN*

Now, let any vector be represented in different basis, thus, this equality will hold true
a ⋅ *u1* + b ⋅ *u2* + ... + z ⋅ *u[N+1]* = A ⋅ *v1* + B ⋅ *v2* + ... + Z ⋅ *vN*

As B is a basis, uniqueness and linear independence holds true in that case, which means we can compare coefficients
a⋅x1 + b⋅y1 + ... + z⋅z1 = A
.
.
.
a⋅xN + b⋅yN + ... + z⋅zN = Z
where symbols with a numerical "subscript" are constants while a, b, ... z are variables (n+1 of them)
Now, we have N+1 variables and N equations.
Imagine a case of two variables and 1 equation (every <N+1 var N eq> case can be reduced to that>
say, x + y = 5, it has infinite solutions (every point on that line in cartesian plane)

Which means if we select B' as our basis, then we can represent the same vector in infinitely many ways, which violates uniqueness and it cannot be our basis. Thus, number of elements in our basis must be the same as B (not lower as dim(span B') decreases).

I guess this works. Does it?

In a linear algebra fashion, i would have wanted to go for a transformation matrix which preserves number of vectors and then show redundancy, but I am not sure how to prove everything along that path.

[LoveDoctorNL]

We have clearance Clarence.
Roger Roger!
What’s our vector Victor?

[aner_bda]

This video would have helped me so much in my first-year physics courses at uni!

[BSpkTKD]

I love the way you teach, the way you encourage us to investigate for ourselves to deepen and reinforce our knowledge, and the way you make your sponsors attractive.
You really know about pedagogy and the way the human mind works when learning, being evident in the means you use to convey your ideas.
You are an inspiration for me, because I want to be build myself to be a teacher in the future.

Thanks for your content!

[carbonsiren]

Love that you're doing this! I'm one of those students who didn't get any real intuition from their linear algebra classes, and after one semester I can only remember some concepts sparsely. Thanks

[woulg]

I really loved 3blue1browns series about linear algebra, but I think you're doing it better hahah. But both are amazing, great work :)

[caspermcgonagle]

Thank you for making this I haven’t taken it yet but the way I’ve heard people talk about it I was genuinely scared going in.

[adityakhanna]

1:05
I can relate to that so much. Certainly the effort put and output are disproportionate, but for some reason one feels so proud of that creation. This is impossible to convey to the viewer. They shall never share our love for the ephemeral object but we know that thing deserves its own video.

[yovangrbovic]

Fuar this might be even better than the strang lectures and 3b1b vids!! Thank you for some awesome content!

[minandychoi]

Lol love the bra-ket vectors in the corners!

[chiragjain]

Maam, if I am not not wrong, vector is any physical quantity which has magnitude and direction. But by this defination electric current also is a vector. But it is not. I think, the quantities for being a vector, should obey the laws of vector addition.

[zvexevz]

This is a great video, very clear. But I have no clue how to solve that question on Brilliant about finding the redundant vector from the set. How is it possible to figure that out without knowing what the basis are? Help!

[ryanjenkinson]

:O
cant wait for the quantum computing stuff :)

A nice proof for part 1 that involves a bit more linear algebra than you gave in the video: Let a basis B = {|v_1>, ..., |v_n>} (may aswell use Dirac notation since it's your favourite). Then the identity map is Id = |v_1 X v_1> + ... + |v_n X v_n> and the trace is trace(Id) = n. Since trace is basis independent, all bases have the same size (namely n).

[rizwansabir]

after the 1 miunutes of this video ... i am here to comment " it is the best video i had watch so far" luv ya