filmov
tv
RIGHT ENDPOINT RULE | Estimate the area under the graph f(x)=1/x from x=1 to x=2 four rectangles

Показать описание
Estimate the area under the graph of f(x)=1/x from x=1 to x=2 using four approximating rectangles and right endpoints. In this video I'll show you how to estimate the area under the graph using four approximating rectangles and right endpoints. Of course, this same technique can be applied for any number of estimating rectangles. And the process for left endpoints and midpoints is similar too. I'll show you how to estimate the area under this curve with the right endpoint formula, also known as the right endpoint Riemann sum equation.
RECOMMENDED READING
0:00 Intro - Estimate the area under the graph
0:25 Right endpoint Riemann sum equation
1:59 Determine pieces of the right endpoint formula
3:37 Plug i values into the right endpoint formula sum
7:06 Add up all terms representing rectangle areas
WATCH NEXT
YOU MIGHT ALSO BE INTERESTED IN...
Some links in this video description may be affiliate links meaning I would get a small commission for your purchase at no additional cost to you.
RECOMMENDED READING
0:00 Intro - Estimate the area under the graph
0:25 Right endpoint Riemann sum equation
1:59 Determine pieces of the right endpoint formula
3:37 Plug i values into the right endpoint formula sum
7:06 Add up all terms representing rectangle areas
WATCH NEXT
YOU MIGHT ALSO BE INTERESTED IN...
Some links in this video description may be affiliate links meaning I would get a small commission for your purchase at no additional cost to you.
Riemann Sums - Left Endpoints and Right Endpoints
RIGHT ENDPOINT RULE | Estimate the area under the graph f(x)=1/x from x=1 to x=2 four rectangles
Estimate the area under 1/x with left endpoint and right endpoint approximation
Riemann sums with right endpoints
Area estimate right endpoints
Approximating Area Under A Curve Using Rectangles and Right Endpoints
Right endpoint estimate of area under a linear function.
Left and right endpoint approximations
Estimating Area using Rectangles | Left Endpoints Rule, Right Endpoints Rule & Midpoint Rule
Area Problem - Riemann Sums - Left Endpoints - Right Endpoints | Calculus
Midpoint Rule & Riemann Sums
Estimating Area Under the Curve using Left/Right Endpoint Reimann Sums
Right hand riemann sum approximation
Numerical Integration 2: Right Endpoint and Midpoint Approximations
Riemann Sum: Left Endpoint & Right Endpoint Rectangles
Left, Right, & Midpoint Riemann Sum Formulas
Approximate Integration-Right end point rule-Lesson-6
Left and right endpoint approximations (edited)
Riemann Sums - Left Endpoints - Right Endpoints | Estimate area Under y = sin x | Calculus
Estimating area under a curve using right-hand end points
Calculus 1 Lecture 4.3: Area Under a Curve, Limit Approach, Riemann Sums
5.1.1 Estimate Area Under Curve (Left Endpoint, Right Endpoint, Midpoint Approximation)
Calculus I: Approximating area under the curve using rectangles
LEFT ENDPOINT RULE | Estimate the area under the graph f(x)=1/x from x=1 to x=2 four rectangles
Комментарии
 0:20:10
0:20:10
 0:07:47
0:07:47
 0:06:42
0:06:42
 0:15:41
0:15:41
 0:03:43
0:03:43
 0:05:41
0:05:41
 0:08:31
0:08:31
 0:16:57
0:16:57
 0:14:04
0:14:04
 0:22:05
0:22:05
 0:11:40
0:11:40
 0:05:29
0:05:29
 0:03:19
0:03:19
 0:08:49
0:08:49
 0:07:23
0:07:23
 0:08:32
0:08:32
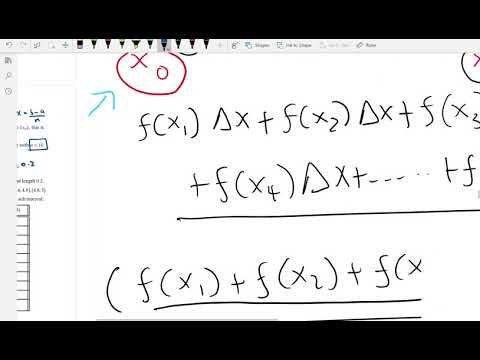 0:07:44
0:07:44
 0:13:02
0:13:02
 0:20:21
0:20:21
 0:07:01
0:07:01
 2:07:03
2:07:03
 0:53:36
0:53:36
 0:09:23
0:09:23
 0:06:39
0:06:39