filmov
tv
Negative Numbers
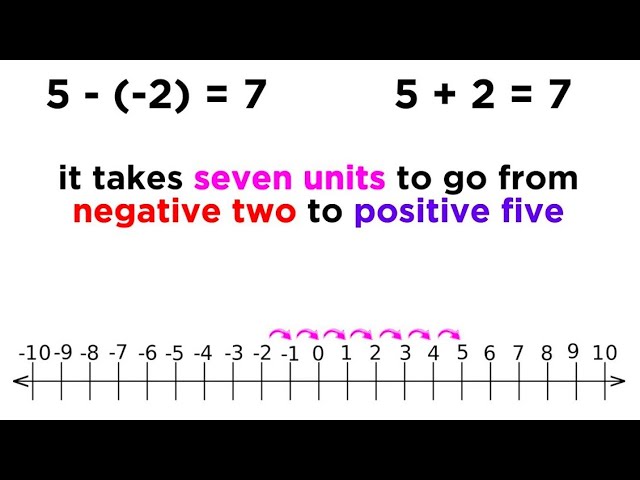
Показать описание
We figured out how to use numbers a long time ago, but then the concept of negative numbers came about. This is a much more abstract concept, because you can't have a negative amount of apples, or something like that. Nevertheless, negative numbers are ubiquitous in math, so we had better learn all about them!
Check out "Is This Wi-Fi Organic?", my book on disarming pseudoscience!
Check out "Is This Wi-Fi Organic?", my book on disarming pseudoscience!
Math Antics - Negative Numbers
A Trick for Adding and Subtracting Negative Numbers
Negative Numbers
Negative Numbers: An Overview
Adding and subtracting negative numbers
Positive and Negative Numbers for Kids | Homeschool Pop
Negative numbers introduction | Negative numbers and absolute value | Pre-Algebra | Khan Academy
How to Subtract Negative Numbers | Subtracting Negative Numbers
How to Add Negative Numbers | Adding Negative Numbers (Integers)
Negative Numbers
Adding and subtracting negative numbers | Pre-Algebra | Khan Academy
Learn The Positive and Negative Numbers – Easy TIP To Remember The Rules!
Why Geniuses were Confused about Negative Numbers ?
Why a negative times a negative is a positive | Pre-Algebra | Khan Academy
Adding and Subtracting Negative Numbers
Math Antics - Adding & Subtracting Integers
Math hacks: Adding Integers | adding negative numbers #integers #negetive #algebra #math #maths
#Maths shorts#Positive and negative rules#*
Adding Positive and Negative Numbers
Introduction to negative numbers
Understanding how positive and negative numbers interact
Multiplying Integers | Positive and Negative Numbers #maths #mathstricks #multiplication #tutorial
Illustrating Why a Negative Times a Negative is a Positive Using the Number Line!
Adding positive and negative numbers
Комментарии
 0:08:27
0:08:27
 0:02:01
0:02:01
 0:05:27
0:05:27
 0:01:51
0:01:51
 0:00:48
0:00:48
 0:08:13
0:08:13
 0:09:36
0:09:36
 0:05:00
0:05:00
 0:04:02
0:04:02
 0:16:23
0:16:23
 0:04:07
0:04:07
 0:14:30
0:14:30
 0:06:38
0:06:38
 0:05:47
0:05:47
 0:09:01
0:09:01
 0:11:23
0:11:23
 0:00:10
0:00:10
 0:00:05
0:00:05
 0:00:37
0:00:37
 0:03:04
0:03:04
 0:03:38
0:03:38
 0:00:12
0:00:12
 0:00:53
0:00:53
 0:00:26
0:00:26