filmov
tv
Algebra Adventure: Conquering Exponential Equations with Ease!
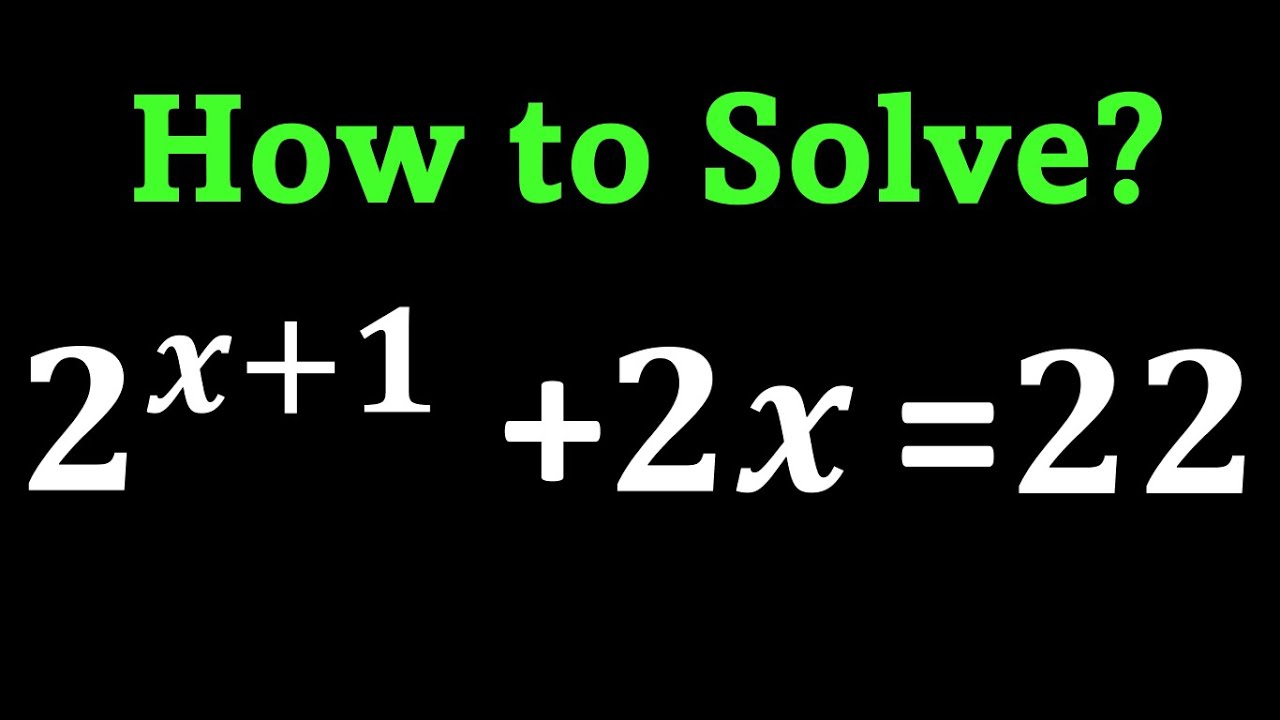
Показать описание
Algebra Adventure: Conquering Exponential Equations with Ease!
In this exciting algebraic adventure, we take on the challenge of solving exponential equations and provide you with the tools and techniques to conquer them with ease. Join us as we unravel the mysteries of exponential equations and guide you through a step-by-step process to solve them confidently. Whether you're a student struggling with algebra or someone looking to sharpen your problem-solving skills, this video is packed with valuable insights and strategies. Discover the power of logarithms, exponential properties, and other algebraic concepts that will help you crack even the most complex exponential equations. Get ready to embark on this educational journey and witness your confidence soar as you overcome these algebraic challenges. Watch now and become an exponential equation-solving master!
Topics covered:
Algebra challenging problem
Exponential Equation
Lambert W function
Graphs
Math Olympiad preparation
Mathematics Challenging equations
Problem solving
#AlgebraAdventure #ExponentialEquations #MathMadeEasy #MathTips #ProblemSolving
8 Key moments of this video :
0:00 Introduction
0:48 Exponent rules
1:33 Substitution
2:32 Algebraic manipulation
2:57 Lambert W Function
5:40 Solving for x
7:01 Graphical conclusions
7:17 Solution using Calculus
Don't forget to subscribe to my channel for more insightful math tutorials and problem-solving techniques! Hit that subscribe button and turn on the notification bell to stay updated with the latest videos on solving exponential equations, logarithms, and other fascinating math topics. Join our community of math enthusiasts and learners, and together, let's unlock the secrets of mathematics!
Thanks for watching !!
@infyGyan
In this exciting algebraic adventure, we take on the challenge of solving exponential equations and provide you with the tools and techniques to conquer them with ease. Join us as we unravel the mysteries of exponential equations and guide you through a step-by-step process to solve them confidently. Whether you're a student struggling with algebra or someone looking to sharpen your problem-solving skills, this video is packed with valuable insights and strategies. Discover the power of logarithms, exponential properties, and other algebraic concepts that will help you crack even the most complex exponential equations. Get ready to embark on this educational journey and witness your confidence soar as you overcome these algebraic challenges. Watch now and become an exponential equation-solving master!
Topics covered:
Algebra challenging problem
Exponential Equation
Lambert W function
Graphs
Math Olympiad preparation
Mathematics Challenging equations
Problem solving
#AlgebraAdventure #ExponentialEquations #MathMadeEasy #MathTips #ProblemSolving
8 Key moments of this video :
0:00 Introduction
0:48 Exponent rules
1:33 Substitution
2:32 Algebraic manipulation
2:57 Lambert W Function
5:40 Solving for x
7:01 Graphical conclusions
7:17 Solution using Calculus
Don't forget to subscribe to my channel for more insightful math tutorials and problem-solving techniques! Hit that subscribe button and turn on the notification bell to stay updated with the latest videos on solving exponential equations, logarithms, and other fascinating math topics. Join our community of math enthusiasts and learners, and together, let's unlock the secrets of mathematics!
Thanks for watching !!
@infyGyan
Комментарии
 0:09:13
0:09:13
 0:08:35
0:08:35
 0:11:51
0:11:51
 0:12:22
0:12:22
 0:02:11
0:02:11
 0:10:58
0:10:58
 0:08:36
0:08:36
 0:07:44
0:07:44
 0:05:11
0:05:11
 0:00:57
0:00:57
 0:08:22
0:08:22
 0:10:54
0:10:54
 0:00:53
0:00:53
 0:01:39
0:01:39
 0:01:46
0:01:46
 0:00:50
0:00:50
 0:02:13
0:02:13
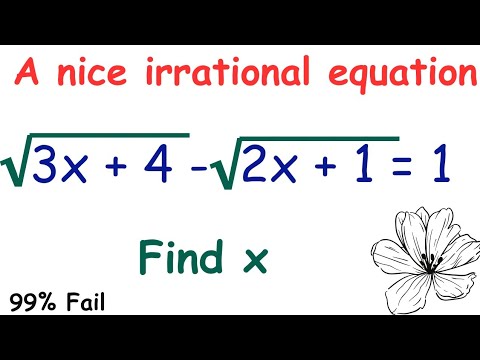 0:05:56
0:05:56
 0:08:35
0:08:35
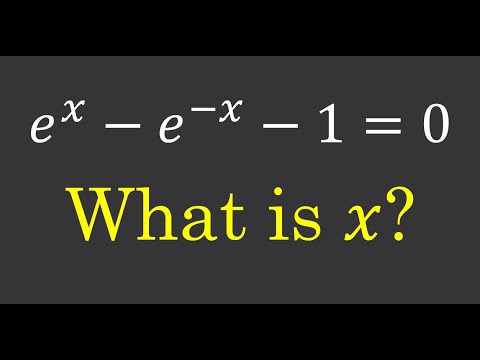 0:06:52
0:06:52
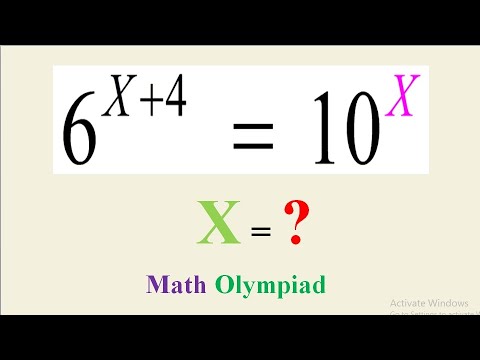 0:08:57
0:08:57
 0:00:55
0:00:55
 0:10:03
0:10:03
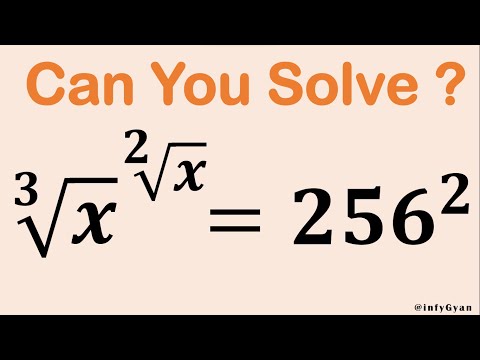 0:11:57
0:11:57