Webinar-The slice representation and the index conjecture for symmetric spaces - Carlos Olmos

Geometry Webinar AmSur/AmSul

Speaker: Carlos Olmos-UNC

Title: The slice representation and the index conjecture for symmetric spaces

Abstract:

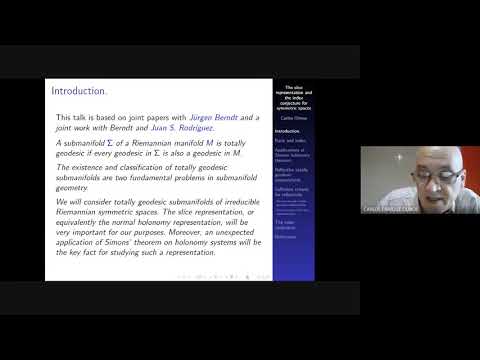
We will speak about results obtained in cooperation with Jürgen Berndt and with Berndt and Juan Sebastián Rodríguez.

A submanifold N of a Riemannian manifold M is totally geodesic if every geodesic in N is also a geodesic in M. The existence and classification of totally geodesic submanifolds are two fundamental problems in submanifold geometry. We will consider totally geodesic submanifolds of irreducible Riemannian symmetric spaces. No complete classifications are known for totally geodesic submanifolds in irreducible Riemannian symmetric spaces of rank greater than two. The classification problem is hopeless unless one restricts to maximal totally geodesic submanifolds. The classification of such maximal submanifolds is an open major question in this classical subject.

In order to gain some insight into this problem there were proposed some simplifications.
In 1980, Onishchik introduced the index of a Riemannian symmetric space as the minimal codimension of a (proper) totally geodesic submanifold. He calculated the index for symmetric spaces of rank less than or equal to 2, but for higher rank it was unclear how to tackle the problem. Some years ago we proposed a new and geometric approach to the index problem based on the study of the slice representation. We found an application of Simons theorem on holonomy systems that was very important for our purposes. By means of this approach we were able, in several papers. to prove the so-called index conjecture which allowed us to determine the index of all symmetric spaces.