filmov
tv
Factoring Quadratics with the Magic Method (when 'a' is NOT 1)

Показать описание
This is the easiest and most efficient way to factor. The magic factoring method can be used to factor any polynomial in the form ax^2+bx+c. This includes quadratic equations when the coefficient "a" is not 1. This way you only need to learn one method to factor. I've noticed that students make fewer mistakes with this method as opposed to using the "magic x."
FACTORING STEPS
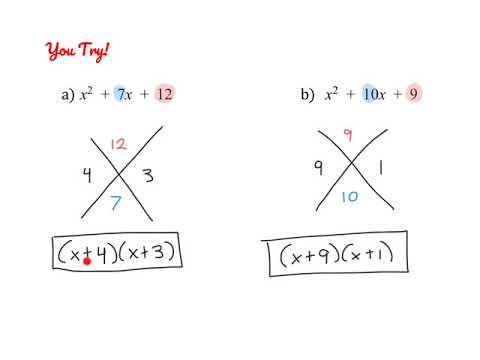
1) Write the a, b, and c values. Remember the standard form of a quadratic expression is ax^2 + bx + c
2) Multiply a • c
3) Find all the factors of the number from step 2
4) Circle the magic pair of numbers whose sum (+) equals the “b” term
5) Write 2 fractions. Use the “a” term as the numerator and each magic factor as a denominator.
6) Simplify each fraction. It is okay if the fraction is improper.
7) Write your answer in the form ( #x + # ) ( #x + # ). The numerator is used as the x coefficient and the denominator is the constant.
8) Check by distributing. You should get the starting expression.
Algebra Common Core A.SSE.3a
FACTORING STEPS
1) Write the a, b, and c values. Remember the standard form of a quadratic expression is ax^2 + bx + c
2) Multiply a • c
3) Find all the factors of the number from step 2
4) Circle the magic pair of numbers whose sum (+) equals the “b” term
5) Write 2 fractions. Use the “a” term as the numerator and each magic factor as a denominator.
6) Simplify each fraction. It is okay if the fraction is improper.
7) Write your answer in the form ( #x + # ) ( #x + # ). The numerator is used as the x coefficient and the denominator is the constant.
8) Check by distributing. You should get the starting expression.
Algebra Common Core A.SSE.3a
 0:09:14
0:09:14
 0:08:56
0:08:56
 0:00:55
0:00:55
 0:03:58
0:03:58
 0:04:17
0:04:17
 0:10:46
0:10:46
 0:05:40
0:05:40
 0:04:04
0:04:04
 0:02:45
0:02:45
 0:05:23
0:05:23
 0:01:23
0:01:23
 0:10:57
0:10:57
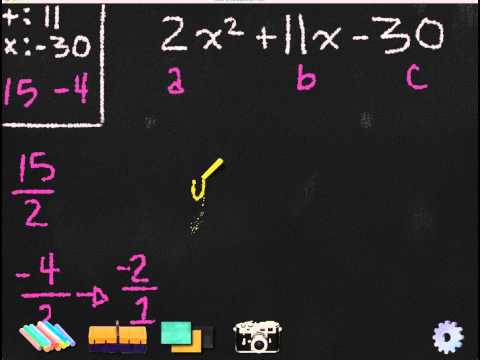 0:02:24
0:02:24
 0:02:12
0:02:12
 0:10:52
0:10:52
 0:10:22
0:10:22
 0:09:22
0:09:22
 0:14:24
0:14:24
 0:01:01
0:01:01
 0:09:10
0:09:10
 0:01:36
0:01:36
 0:03:35
0:03:35
 0:22:38
0:22:38
 0:08:30
0:08:30