Circle perimeter and area from polygons

Estimates pi from polygons. Shows that perimeter/2r approaches pi (π), as number of sides of polygon increases (approaching a circle). It's true for circles of any radius (r), which you can test by varying radius here:

You also can set a turn angle and press "T" for a test by making a polygon and then sending around a white sprite that, using no trig, moves the calculated side length while turning the degrees you chose. (The orientation is the trigonometry style, counterclockwise angles, with 0 degrees facing east).

We did all this with Scratch code blocks, so it's a good way to learn coding and beautiful math at the same time.

Note that this draws not a true circle but a polygon with very many tiny flat sides. The very tiny flat side length is the key to estimating pi (and radians per degree as .01745).

The model increases # sides of polygon, updating perimeter and (outer) side length. This estimates pi as 3.1415... and estimates radian length for 1 degree = 0.01745 = side length / r, when turn angle = 1.

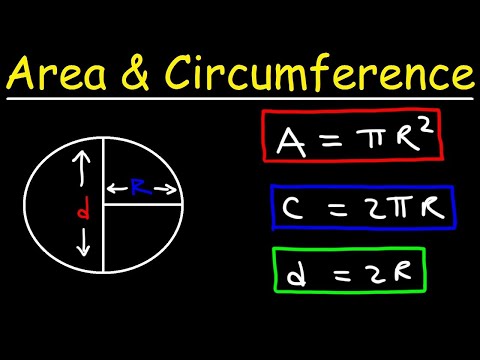
A circle's circumference = π2r = π*diameter, suggesting polygons with very many sides should have a perimeter close to a circle's circumference.

The model suggests circle is a polygon with infinite number of sides, but we stop at 1 degree turns which makes a 360 sided polygon called a "trihectohexacontagon."

#areaofcircle #perimeterandarea #polygons #beautifuldiscoverymodeling