Differential Geometry: Lecture 15 part 3: Gaussian and Mean curvature

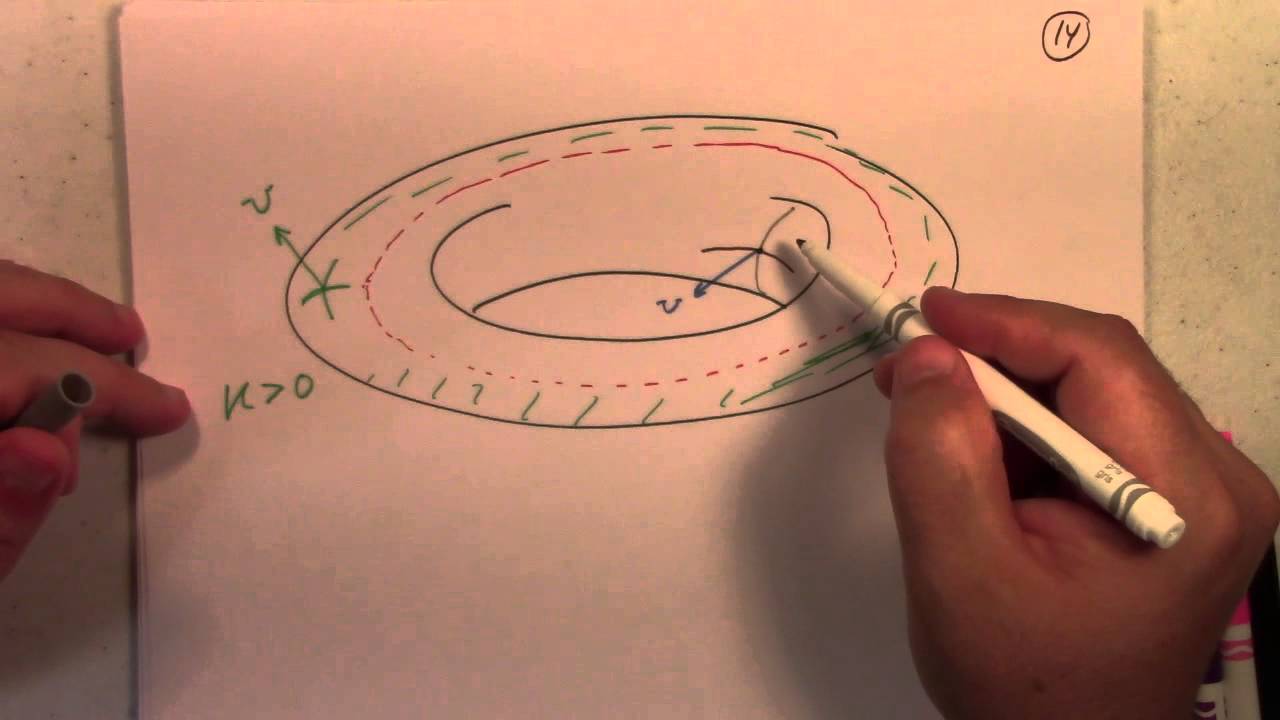
The determinant and trace of the shape operator are used to define the Gaussian and mean curvatures of a surface. We also derive Lagrange's identity and use it to derive a pair of involved formulas which are needed for the alphabet soup of the next section. Finally, the terms "flat" and "minimal" are introduced. However, minimal is not motivated or explained here (see Section 3D of Kuhnel for a really interesting discussion with neat examples)

[jceradnac]

how do we calculate for the critical points of the gaussian and mean curvature? Do we just find where those expressions become zero?

[nicholasroberts]

practice problems for finding gaussian curvature?

[rachinodo]

personally think very kindly saying than the others

[KJKP]

At 32:22, the second term should be negative, (-k1k2)/2