filmov
tv
the failure of integration by parts!

Показать описание
🌟Support the channel🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
the failure of integration by parts!
this is how students failed calculus 2
Math Integration Timelapse | Real-life Application of Calculus #math #maths #justicethetutor
This is how students failed calculus
This is how students failed calculus
how students failed calc 3
Failure is Part of Mathematics #shorts
This is Worse than Failure
How To Enable/Disable Integration Failure Email Notification Global Fluent Forms
EU economic integration strategy for Eastern Europe 'has failed': Heiner Flassbeck
Integration, Segregation, Assimilation and the Mechanization of Failure
[BBST 465] The Marks of Failed Integration - Rick Langer
A Breathtaking Journey of Integration
Failure Breeds Success
Trying to stay diplomatic about a transformation failure... but sometimes the truth just gets said
NEW footage emerges of fairground ride falling apart 👀
What Happened to Google+
😍National Crush of JEE Aspirants🇮🇳 #iit #motivation #iitdelhi
What no one openly talks about: the silent discrimination of Central and Eastern Europeans in WE
Why the S 400 Succeeded in India but Failed in Russia
Multiculturalism HAS FAILED!
I FAILED CALCULUS
Never give up #ronmalhotra #failure #nevergiveup
Solving the Failed to resolve anonymous Party during integration test Issue in Corda
Комментарии
 0:18:33
0:18:33
 0:00:09
0:00:09
 0:00:09
0:00:09
 0:00:07
0:00:07
 0:00:11
0:00:11
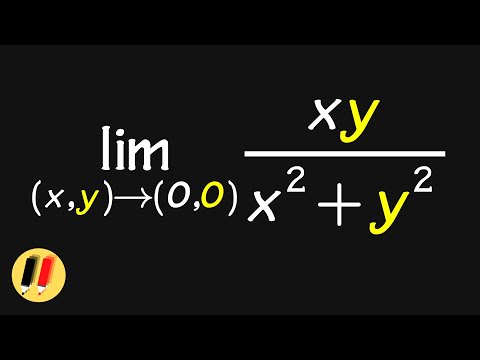 0:00:24
0:00:24
 0:00:21
0:00:21
 0:00:31
0:00:31
 0:00:41
0:00:41
 0:03:08
0:03:08
 2:11:45
2:11:45
![[BBST 465] The](https://i.ytimg.com/vi/Fs7dG9VkKB4/hqdefault.jpg) 1:01:46
1:01:46
 0:12:19
0:12:19
 0:00:44
0:00:44
 0:00:09
0:00:09
 0:00:28
0:00:28
 0:00:50
0:00:50
 0:00:35
0:00:35
 0:00:54
0:00:54
 0:06:13
0:06:13
 0:01:01
0:01:01
 0:00:41
0:00:41
 0:00:09
0:00:09
 0:02:10
0:02:10