Algebra 65 - Creating Quadratic Expressions Using the FOIL Method

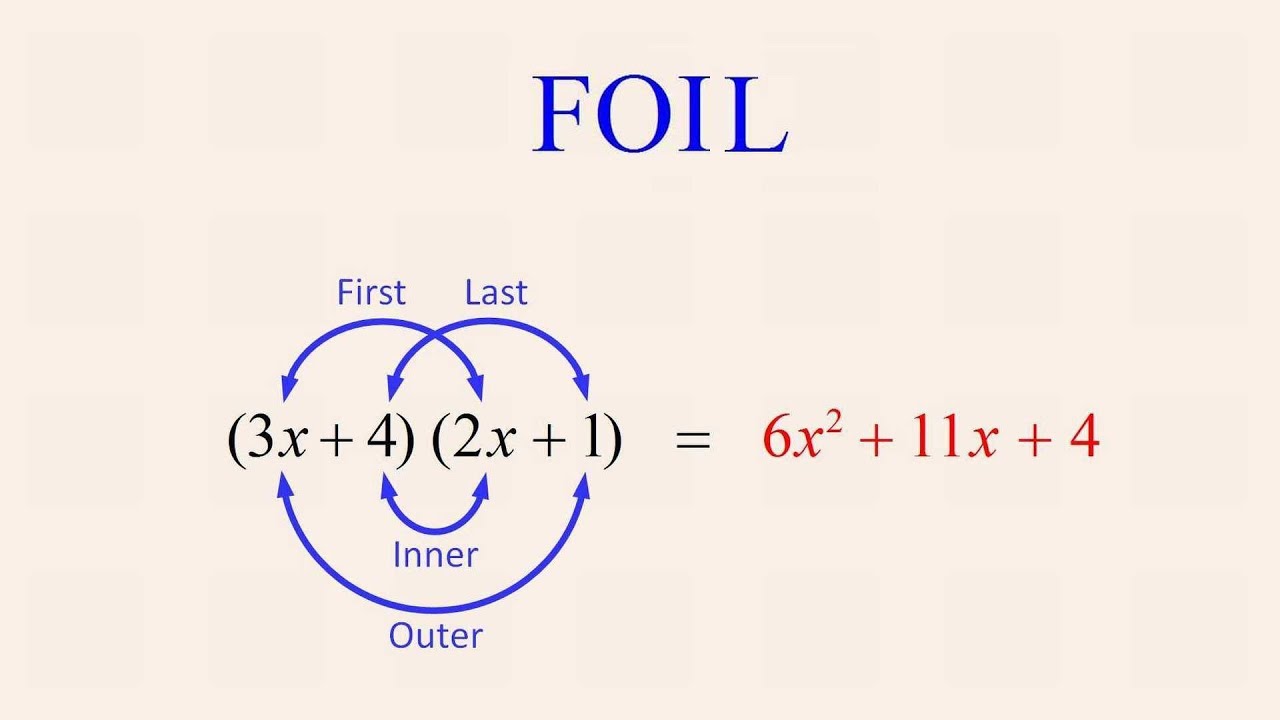
Quadratic expressions may be created by multiplying two linear binomial expressions together. A common procedure for multiplying two binomial expressions is referred to as the "FOIL" method. FOIL is an acronym whose letters stand for the four terms produced by the products of the First, Outer, Inner, and Last terms of the two binomials.

[aryanjhariya]

Hey man don't ever stop making videos because some one is watching your every video understand.

[coffeedesbeans]

I wish I could've found your video in the beginning of the semester. Like everything makes perfect sense now.

[shxn]

You definitely deserve more likes man👁️💧👄💧👁️
You saved me grades👁️💧👄💧👁️👍

[marxiusivanadolfdenniellom]

My school took 2 weeks teaching me this and i understood nothing.
And you teached me this for 2 minutes and i instantly learned it

[ericthiel]

I keep messing this up. All through highschool and now in calculus in college. Frustrating but I thank you for the vids. Definitely help with homework. If I could just get it down without looking....

[operatormiku]

thank you so much! as a visual learner, this helped me out a ton.

[jkgan]

I really don't understand why students are taught the FOIL method. It's not really something you need to remember with an acronym. You are just distributing one of the factors into the other. For example:
(3x + 4) (2x + 1) = [ 2x (3x + 4) + 1 (3x + 4) ]
and then we distribute one more time,
= (2x) (3x) + (2x) (4) + (1) (3x) + (1) (4)
This turns out to give the exact same terms as the FOIL method did.

The (3x + 4) went into the other set of brackets because of the distributive property. You can distribute the other set of brackets "(2x + 1)" in you want; it doesn't make a difference. Maybe students don't like the fact when you distribute something with two or more terms. But it makes sense. For example:
3 (1 + 2) = (1) (3) + (2) (3)
or we can say the following:
(2 + 1) (1 + 2) = [ 1 (2 + 1) + 2 (2 + 1) ]
Instead of distributing a 3, we can break up the 3 into two terms and distribute a (2+1) instead.

Edit: You can also extend this to a (trinomial * trinomial). For example:
( a + b + c) ( x + y + z) = [ x (a + b + c) + y (a + b + c) + z (a + b + c) ]
In this case, your FOIL method won't really help you, so it's better to just understand why it works. This used to cause me some confusion, so I just decided to leave this here. Ok, I'm done now :)

[robertjarman]

You mentioned long ago that you can see how the three variable systems where that brainiac kid was using that slingshot, you said that the height can be found via vertex form. I'm interested in how that happens. Also, will you go over the various types of regressions and exponential expressions?

[johnargiropolis]

Tired of hearing people disparage FOIL, they want us to say, "distribute". FOIL is just a mnemonic device that places the terms in a convenient order for simplification. One can prove FOIL in a few steps using Closure of Addition and the Distributive Property. There are several mnemonic devices in mathematics; even as high as calculus (lo-dee-hi minus hi-dee-lo over lo squared) and in the 30 years that I've taught mathematics, appeared to be beneficial to students.

[knifeandtongue]

salamat sa diyos nagegets ko na konti konti