filmov
tv
Algebra 67 - Deriving the Vertex Form of a Quadratic Function
Показать описание
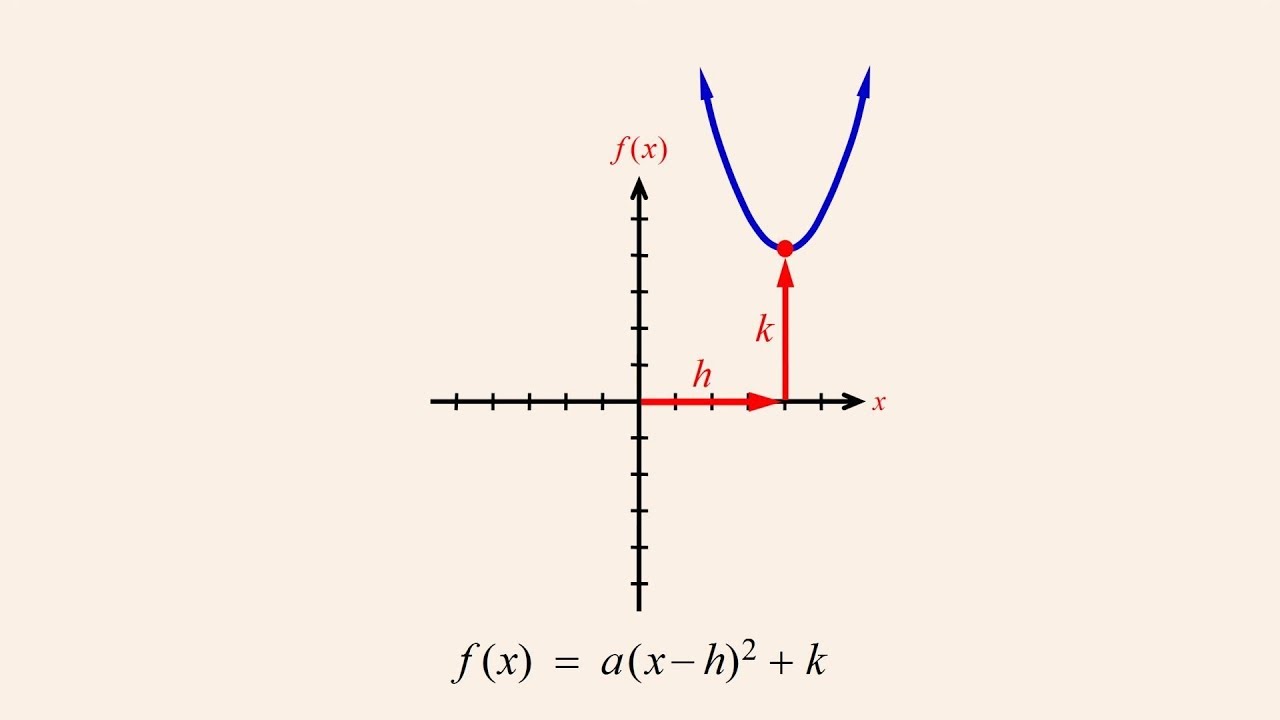
The graph of a quadratic function in a single variable is always a parabola, and when the function is written in vertex form, we can identify the coordinates of the parabola's vertex simply by looking at the function. But how is the vertex form derived and why does it work? The process explored here involves shifting or 'translating' the basic quadratic function "a x-squared".
Algebra 67 - Deriving the Vertex Form of a Quadratic Function
67+89🥵#matemática #short #shorts #algebra #educación #shortsvideo
PreCalculus - Algebra Fundamental Review (67 of 80) 6 Ways to Graph a Parabola 1) Table of Values
Two Ways to Rewrite Fractional Exponents into Radicals #Shorts #algebra #math
🤩Laws Of Exponents/ Algebra Rules #algebra #shorts #trending #exponents #artikipathshala #shortsfeed...
Abstract Algebra 67: The number of rotational symmetries of a soccer ball
GCSE Maths - What on Earth is y = mx + c #67
Writing the equation of a parallel line #math #algebra #geometry #shorts
Solve z-67=16: Linear Equation Video Solution | Tiger Algebra
Least Squares Solutions and Deriving the Normal Equation | Linear Algebra
Square Trick for no.67#shorts #squaretrick #viralshorts #shortvideo #algebra class #67
Solving for x in 2ˣ = (1/8) #Shorts #algebra #math #maths #mathematics #education #learn #learning
Solving An Exponential System | Algebra
important algebra formula
Algebra| Algebra Shortcuts| Algebra Tricks in Hindi| Algebra Math Tricks| Maths for SSC CGL |
67^67+67 divided by 68 Algebra Class 11 Best Trick Competitive Exam ||SSC ||RAILWAY||BANKING||UPSC
algebra ka jod ghatav guna bhag। short video NTPC Baink railway for all exams
Algebra 2 Lesson #67 How to Solve Quadratic and Rational Inequalities
Slope Field In Exercises 67-72, use a computer algebra system to (a) graph the slope field for the …...
Solve 8x-7=67: Linear Equation Video Solution | Tiger Algebra
Lecture 67: Linear Algebra (Interesting example from a car factory)
intermediate algebra 67
Solving for x in x³ - 11 = 53 #Shorts #algebra #math #maths #mathematics #education #learn #learning...
Solve 67-5c=-28: Linear Equation Video Solution | Tiger Algebra
Комментарии
 0:09:25
0:09:25
 0:00:14
0:00:14
 0:06:41
0:06:41
 0:00:14
0:00:14
 0:00:16
0:00:16
 0:09:16
0:09:16
 0:04:53
0:04:53
 0:00:44
0:00:44
 0:00:42
0:00:42
 0:25:06
0:25:06
 0:00:17
0:00:17
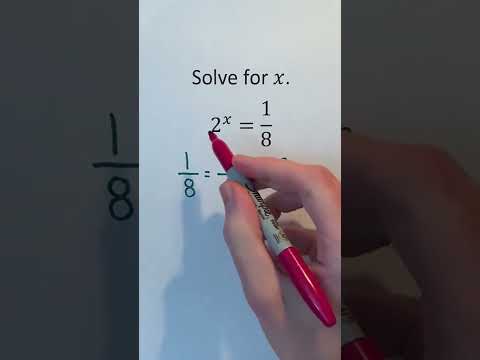 0:00:30
0:00:30
 0:00:44
0:00:44
 0:00:19
0:00:19
 0:00:46
0:00:46
 0:02:42
0:02:42
 0:00:16
0:00:16
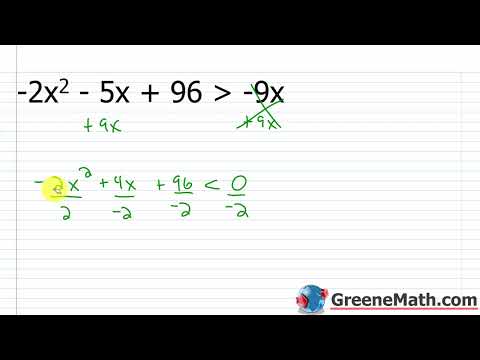 0:32:06
0:32:06
 0:00:33
0:00:33
 0:01:07
0:01:07
 0:13:23
0:13:23
 0:07:12
0:07:12
 0:00:16
0:00:16
 0:01:20
0:01:20