Reconnection number of vortex knots - Louis H Kauffman

Topological Methods in Mathematical Physics 2022
International Conference

Title: Reconnection number of vortex knots

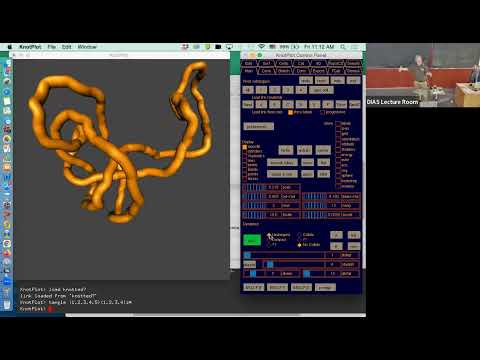
Abstract: Knotted vortices such as those produced by Kleckner and Irvine at the Frank Institute of the University of Chicago tend to transform by reconnection to collections of unknotted and unlinked circles [1], [2]. The reconnection number R(K) of an oriented knot of link K is the least number of reconnections (oriented re-smoothings) needed to unknot/unlink K. Putting this problem into the context of knot cobordism, we show, using Rasmussen’s Theorem ([3], [4], [5]) that the reconnection number of a positive knot is equal to twice the genus of its Seifert spanning surface. In particular an (a,b) torus knot has R = (a-1)(b-1). For any knot or link diagram K, we show that R(K) is counted from above by c(K) - s(K) + 1 where c(K) is the number of crossings of K and s(K) is the number of Seifert circles of K. For an arbitrary positive knot or link K, this is an equality. That is, for K a positive link, R(K) = c(K) -s(K) + 1. Examples of vortex dynamics will be illustrated.

[1] Kleckner, D. and Irvine, W.T.M. 2013 Creation and dynamics of knotted vortices. Nature Physics 9, 253258.
[2] Kleckner, D., Kauffman, L.H. and Irvine, W.T.M. 2016 How superfluid vortex knots untie, Nature Physics 12, 650655.
[3] Kauffman, L. H. 2016 An introduction to Khovanov homology. In Knot Theory and Its Applications”, p. 105139. Contemp. Math., 670, Amer. Math. Soc., Providence, RI.
[4] Dye, H.A., Kaestner, A. and Kauffman, L.H. 2017 Khovanov homology, Lee homology and a Rasmussen invariant for virtual knots. J. Knot Theory Ramifications 26, 1741001.
[5] Rasmussen, J. 2010 Khovanov homology and the slice genus. Invent Math. 182, 419447.

Keywords: reconnection number, vortex knots