Parametric Equations for a Ladder Sliding Down a Wall (Multivariable Calculus Challenge Problems)

This is similar to Oxford's ladder interview question, which is the topic of a video on the channel Mindyourdecisions related to calculus.

Multivariable Calculus Challenge Problems (with Mathematica Demonstrations), Video #1. Exercise #11.1.66 from the 3rd Edition of "Multivariable Calculus", by Jon Rogawski and Colin Adams.

(0:00) The first of many videos on Challenge Problems from Multivariable Calculus. I will also use Mathematica demonstrations in these videos as well. (2:01) Problem statement. (3:41) Mathematica demonstration (an animation with the Mathematica Manipulate function). (6:22) Solve the challenge problem using the diagram and trigonometry with a right triangle (use SOH CAH TOA for the sine, cosine, and tangent of the angle). (13:04) Show the point P follows the path along an ellipse by using the equation of an ellipse (substitute the parametric equations into it) and the Pythagorean identity (cos^2 + sin^2 = 1 for all input angles). (16:16) Concluding comments.

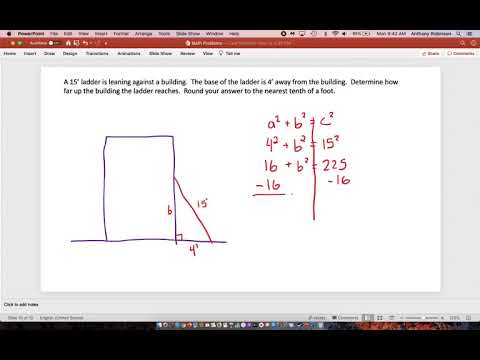
Problem Statement: Rogawski & Adams, Third Edition, #11.1.66: A 10-ft ladder slides down a wall as its bottom B is pulled away from the wall (see figure below). Using the angle theta as a parameter, find the parametric equations for the path followed by (a) the top of the ladder A, (b) the bottom of the ladder B, and (c) the point P located 4 ft from the top of the ladder. Show that P describes (part of) an ellipse.

AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.

[megalith]

Thank you sir, i never understood these problems before. It now feels so logical.