filmov
tv
Can a linear transformation from 2D to 3D be onto?

Показать описание
Can a linear transformation from R2 to R3 be onto?
Check out the follow up video for the solution!
Learn about topics in linear algebra like image, linear transformations, surjectivity, and more!
Made by
Nic Swanson
Follow me on Twitter for more Math related content!
@QualityMathVis
Check out the follow up video for the solution!
Learn about topics in linear algebra like image, linear transformations, surjectivity, and more!
Made by
Nic Swanson
Follow me on Twitter for more Math related content!
@QualityMathVis
Linear transformations and matrices | Chapter 3, Essence of linear algebra
Linear Transformations on Vector Spaces
Linear transformations | Matrix transformations | Linear Algebra | Khan Academy
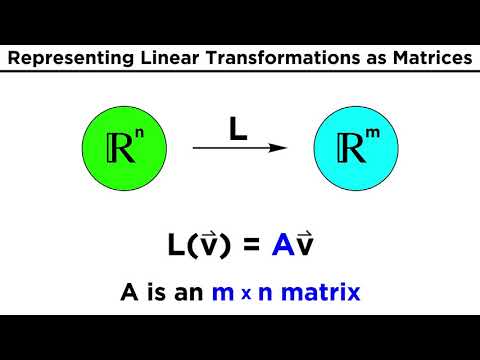
How to Find the Matrix of a Linear Transformation
Image and Kernel
Linear Transformations , Example 1, Part 1 of 2
Oxford Linear Algebra: Linear Transformations Explained
KERNEL and RANGE of a LINEAR TRANSFORMATION - LINEAR ALGEBRA
The Eckart-Young Theorem
Proving a Function is a Linear Transformation F(x,y) = (2x + y, x - y)
[Linear Algebra] Linear Transformations
How to Show a Function is Not a Linear Transformation
Three-dimensional linear transformations | Chapter 5, Essence of linear algebra
Linear Transformations
Linear Algebra 1.8.2 Introduction to Linear Transformations
What is a linear transformation
Linear Transformations
Linear Algebra - Lecture 19 - The Matrix of a Linear Transformation
Linear Algebra: Checking if a transformation is one-to-one and onto
How to Prove a Function is a Linear Transformation
#5||Matrix representation of Linear Transformation||Linear algebra||maths for graduates
Matrix multiplication as composition | Chapter 4, Essence of linear algebra
Linear Transformations: Onto
Linear transformation examples: Scaling and reflections | Linear Algebra | Khan Academy
Комментарии
 0:10:59
0:10:59
 0:09:11
0:09:11
 0:13:52
0:13:52
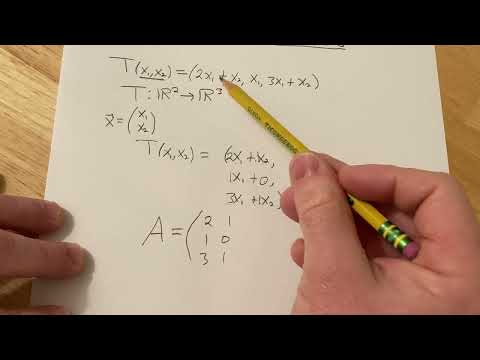 0:05:19
0:05:19
 0:05:35
0:05:35
 0:09:06
0:09:06
 0:32:58
0:32:58
 0:08:46
0:08:46
 0:12:05
0:12:05
 0:07:49
0:07:49
![[Linear Algebra] Linear](https://i.ytimg.com/vi/cFIRXQBfgg0/hqdefault.jpg) 0:12:30
0:12:30
 0:03:04
0:03:04
 0:04:46
0:04:46
 0:11:22
0:11:22
 0:09:23
0:09:23
 0:33:47
0:33:47
 0:10:47
0:10:47
 0:10:44
0:10:44
 0:06:29
0:06:29
 0:07:45
0:07:45
 0:05:32
0:05:32
 0:10:04
0:10:04
 0:08:24
0:08:24
 0:15:13
0:15:13