filmov
tv
Euler's Insight - A Function That Generates Values of the Riemann Zeta Function

Показать описание
In this video I show a particular identity which can be used to solve the Basel problem, as well as find exact forms for the Riemann zeta function evaluated at any positive even number.
Euler's Insight - A Function That Generates Values of the Riemann Zeta Function
What's so special about Euler's number e? | Chapter 5, Essence of calculus
Euler angles - Insights
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
This equation blew my mind // Euler Product Formula
Euler's number e : Defined in diverse ways | Mathematics
What is Euler's Number 'e' & Why is it SO Important?
Math on Shorts: the Beauty of Euler's Formula #EulersFormula #ComplexNumbers
Euler's formula (See NEW: https://youtu.be/DaK2ZSJNcFo), sin & cos in terms of complex expo...
The Euler characteristic: A general topological descriptor for complex data I PyData Chicago 2022
Euler's real identity NOT e to the i pi = -1
Euler's Product for the Zeta function via Boxes I | Math Foundations 240 | N J Wildberger
The Riemann Hypothesis | Ep. 1: The Euler Product
Your Daily Equation #11: Euler's Identity or The Most Beautiful of all Equations
Complex Integration and Finding Zeros of the Zeta Function
Can Euler's Formula Be Understood Before Calculus Class?
Euler's Form of Circular Functions - Hyperbolic Functions - Engineering Mathematics 1
The hardest 'What comes next?' (Euler's pentagonal formula)
Visualizing Complex-Valued Functions
Pythagoras' Theorem edit 🐐🔥 | #shorts #maths
e^(-1+i3pi)/e^(-1+pi/2) Euler's Formula Engineering Analysis
The Beauty of Mathematics #inspiration #themanwhoknewinfinity
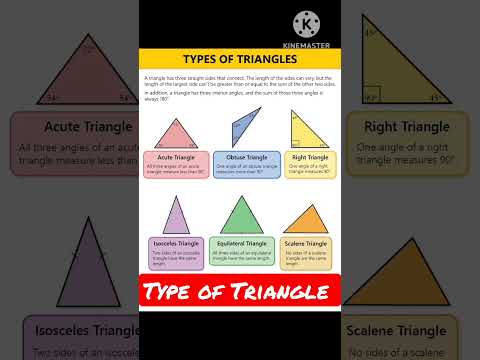
📐 type of triangle 📐
The number e explained in depth for (smart) dummies
Комментарии
 0:44:25
0:44:25
 0:13:50
0:13:50
 0:07:50
0:07:50
 0:00:38
0:00:38
 0:17:04
0:17:04
 0:00:55
0:00:55
 0:42:32
0:42:32
 0:00:59
0:00:59
 0:14:25
0:14:25
 0:47:15
0:47:15
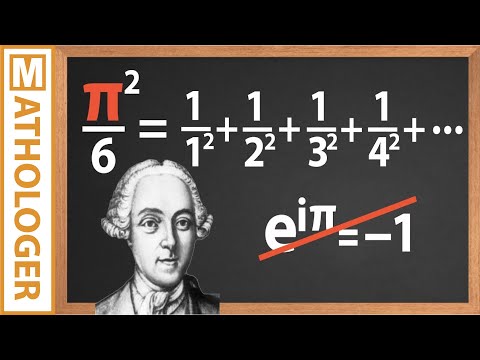 0:17:16
0:17:16
 0:35:45
0:35:45
 0:11:53
0:11:53
 0:26:20
0:26:20
 0:52:49
0:52:49
 0:13:58
0:13:58
 0:04:44
0:04:44
 0:53:33
0:53:33
 0:23:38
0:23:38
 0:00:19
0:00:19
 0:06:41
0:06:41
 0:00:59
0:00:59
 0:00:05
0:00:05
 0:18:38
0:18:38