filmov
tv
math Olympiad questions |Math riddles|math genius #matholympiad #mathriddles #matholympics shorts

Показать описание
Luxembourg - Math Olympiad Question | You should know this trick
9 Math Riddles That'll Stump Even Your Smartest Friends
Math quiz
If you are a genius solve this! Math Game Challenge!!!
Solving the hardest question of a British Mathematical Olympiad
Genius IQ Test-Maths Puzzles | Tricky Riddles | Maths Game | Paheliyan with Answers | Tricky Paheli
Math Quiz That'll Stump Most People (Even Math Nerds)
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
Oxford University Mathematician REACTS to '9 Math Riddles That'll Stump Even Your Smartest...
Can You Solve The Knight On A Chessboard Riddle? Math Olympiad Problem
Viral logic test from Brazil
Genius IQ Test math puzzle🔥
Math Olympiad Question | You should know this trick!!
Insanely Hard High School Math Question - Online Math Olympiad Apple Tree Probability
Norway Math Olympiad Question | You should be able to solve this!
Viral question from China
A math olympiad problem that looks complicated, but it's easy to solve
Challenging Math Olympiad Problem | Geometry Question | Mathematics | 2 Methods
Solving An Insanely Hard Problem For High School Students
math Olympiad questions |Math riddles|math genius #matholympiad #mathriddles #matholympics shorts
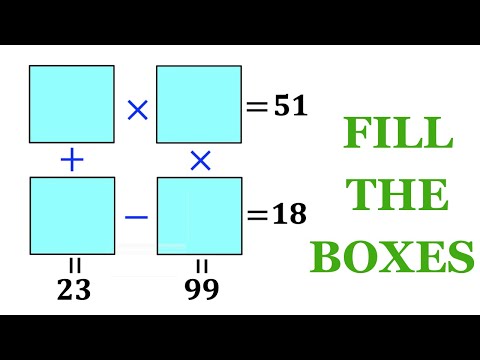
Can you solve this Logic Puzzle? | Fill the Boxes with the right values | Math Olympiad Training
The REAL Answer Explained
logical questions for all classes. #shorts #logicalreasoning #ssccgl #sscchsl
Google AI dominates the Math Olympiad. But there's a catch
Комментарии
 0:02:51
0:02:51
 0:06:40
0:06:40
 0:00:05
0:00:05
 0:00:28
0:00:28
 0:11:26
0:11:26
 0:00:24
0:00:24
 0:05:15
0:05:15
 0:00:52
0:00:52
 0:22:59
0:22:59
 0:06:13
0:06:13
 0:06:41
0:06:41
 0:00:05
0:00:05
 0:00:33
0:00:33
 0:17:48
0:17:48
 0:03:21
0:03:21
 0:08:04
0:08:04
 0:10:23
0:10:23
 0:25:44
0:25:44
 0:07:27
0:07:27
 0:00:08
0:00:08
 0:06:43
0:06:43
 0:07:23
0:07:23
 0:00:12
0:00:12
 0:08:18
0:08:18