filmov
tv
Series of 2^(1/n)-1 with limit comparison test, calculus 2 tutorial

Показать описание
Does this Series Converge or Diverge? Series (2^(1/n)-1)
----------------------------------------
#blackpenredpen #math #calculus #apcalculus
----------------------------------------
#blackpenredpen #math #calculus #apcalculus
Determine if sequence converges or diverges, if converges find limit (-1)^n/(2sqrt(2))
lim n^1/n = 1
Proof: Sequence (n+1)/n Converges to 1 | Real Analysis
Series of 2^(1/n)-1 with limit comparison test, calculus 2 tutorial
Limit of (-1)^n(n/(n + 1))
Find the Limit of SUM((1/n^3)(i - 1)^2) as n approaches infinity
Series of (1+1/n)^(n^2), root test
Series of sin(1/n) diverges, Limit comparison test, calculus 2 tutorial
Chain Rule Shortcut Method of Differentiation | Derivatives #excellenceacademy #jonahemmanuel
Determine if sequence converges or diverges, if converges find limit {(1+ 2/n)^n}
Determining whether a sequence converges or diverges
❖ Finding the Limit of a Sequence, 3 more examples ❖
Evaluate: Lim(n→∞)[1/(n+1)+1/(n+2)+......+1/2n]
Proof: Sequence (3n+1)/(n+2) Converges to 3 | Real Analysis
Limit Comparison Test, Series of 1/(2n+1), calculus 2 tutorial
Sequences (Real Analysis) | SE#12-13 | Monotone convergence theorem | 1/n+1...+1/n+n & 1/1!+...+...
Converging and Diverging Sequences Using Limits - Practice Problems
Calculus 2 - Geometric Series, P-Series, Ratio Test, Root Test, Alternating Series, Integral Test
Determine if sequence converges or diverges, if converges find limit ((-1)^(n+1) n)/(n + sqrt(n))
checking for absolute convergence, series of sin(2n)/(1+2^n), calculus 2 tutorial
How to Determine if a Sequence Converges or Diverges: Example with n*sin(1/n)
Telescoping Series
Calculus 2 Lecture 9.1: Convergence and Divergence of Sequences
Proof that the Sequence (-1)^n Diverges using the Definition
Комментарии
 0:02:10
0:02:10
 0:02:13
0:02:13
 0:06:43
0:06:43
 0:06:47
0:06:47
 0:01:20
0:01:20
 0:06:29
0:06:29
 0:03:23
0:03:23
 0:05:36
0:05:36
 0:01:00
0:01:00
 0:03:21
0:03:21
 0:05:39
0:05:39
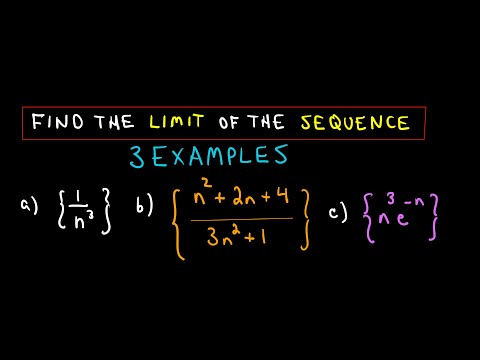 0:03:24
0:03:24
![Evaluate: Lim(n→∞)[1/(n+1)+1/(n+2)+......+1/2n]](https://i.ytimg.com/vi/dYWmswSdF0Q/hqdefault.jpg) 0:03:06
0:03:06
 0:06:53
0:06:53
 0:03:00
0:03:00
 0:05:34
0:05:34
 0:30:13
0:30:13
 0:43:52
0:43:52
 0:03:05
0:03:05
 0:05:36
0:05:36
 0:04:04
0:04:04
 0:23:39
0:23:39
 2:27:29
2:27:29
 0:04:27
0:04:27