filmov
tv
Jensen's Inequality proof

Показать описание
Jensen's Inequality proof
Jensen's Inequality
Lecture 19 (Part 1): Convex function and Jensen's inequality (proof)
Lecture 15 (Part 7): Jensen's inequality with proof and a simple example about making an invest...
S18.2 Jensen's Inequality
Jensen's Inequality Explained: Understanding Convex Functions & The Basics
Proving Jensen's Inequality
18 - Jensens inequality
Cauchy-Schwarz: Proof using Jensen's Inequality
Jensen's Inequality - Short Proof & Example
Jensen's Inequality : Data Science Basics
Using Karamata's Inequality to prove the infamous APMO 1996, problem 5, arbitrary triangle prob...
Jensen's inequality
The intuition behind Jensen's Inequality
Karamata inequality
Jensens Inequality.AVI
Jensen’s Inequality Example
Jensen's Inequality
How to use JENSEN'S INEQUALITY in concave and convex functions to prove trigonometric inequali...
FTiP/7. Jensen's and Ljapunov's inequality
Jensen's Inequality: How to Use It
Jensen inequality application example 2
Trigonometric Inequality with Desmos Visualization: The Secret Behind the Proof
Jensens inequality, advanced maths for London by Vasilis Mpakas.mp4
Комментарии
 0:04:24
0:04:24
 0:06:57
0:06:57
 0:20:44
0:20:44
 0:18:18
0:18:18
 0:12:19
0:12:19
 0:06:44
0:06:44
 0:14:20
0:14:20
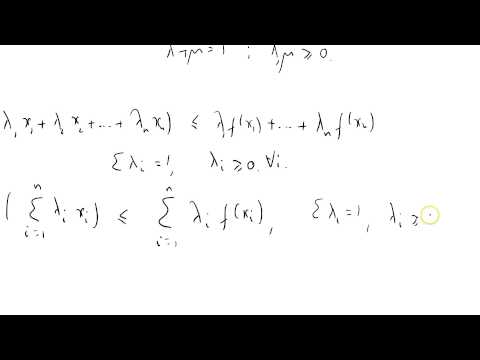 0:03:48
0:03:48
 0:07:59
0:07:59
 0:10:38
0:10:38
 0:18:04
0:18:04
 0:09:16
0:09:16
 0:16:26
0:16:26
 0:06:08
0:06:08
 0:10:42
0:10:42
 0:07:10
0:07:10
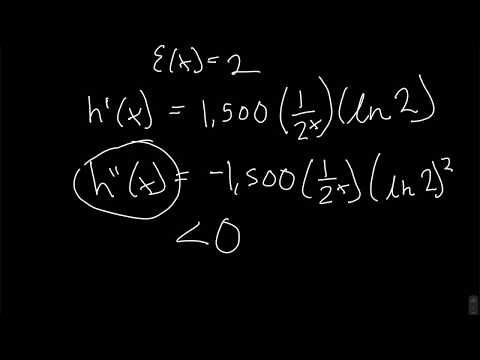 0:11:56
0:11:56
 0:07:45
0:07:45
 0:02:14
0:02:14
 0:13:54
0:13:54
 0:12:53
0:12:53
 0:03:41
0:03:41
 0:03:37
0:03:37
 0:26:42
0:26:42