filmov
tv
de Broglie Law of Phase Harmony='a very special synchronization' Lou Kauffman='2, 3, ∞' Connes music

Показать описание
This is the secret of the Law of Phase Harmony also being noncommutative as John G. Williamson explains:
A new theory of relativistic quantum mechanics explains that Law of Phase Harmony is noncommutative. So in reality this is quantum biology that is relativistic nonlocality as the Tao and the "three gunas."
A new theory of relativistic quantum mechanics explains that Law of Phase Harmony is noncommutative. So in reality this is quantum biology that is relativistic nonlocality as the Tao and the "three gunas."
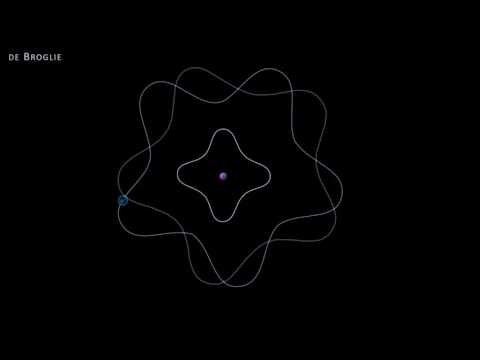
Louis de Broglie's explanation of Bohr's atomic model
Derive De-Broglie Wave Equation | Quantum Chemistry | Physical Chemistry
De Broglie's Hypothesis - The Phase Wave
de Broglie Law of Phase Harmony='a very special synchronization' Lou Kauffman='2, 3, ...
Light Speed stable particles=Protons as de Broglie Law of Phase Harmony Eternal Quantum Black Hole
Wave Model of an Electron
How small are atoms?
Davisson-Germer Experiment & Wave-Particle Duality
DeBroglie hypothesis of matter waves, expression for debroglie wavelength modern physics, quantum P
How much does a PHYSICS RESEARCHER make?
Purdue PHYS 342 L9.7: Statistical Laws of Nature: Thermal de Broglie Wavelength
de Broglie Hypothesis and Wave Nature of Electrons
Dr. William Tiller Dr. Nisha Manek: de Broglie Law of Phase Harmony Negentropy info Yuan Qi healing
Diffraction Pattern of Light by Single Slit Using Two Blades....
The Photoelectric Effect
1st yr. Vs Final yr. MBBS student 🔥🤯#shorts #neet
Aspirants Must Know The Value Of 1 minute #motivation #iitstatus #upscstatus #neetstatus #toppers
Heisenberg Uncertainty Principle😲 - Aisa practical nahi dekha hoga😍#shorts
Before JEE vs After JEE 😍 | My Transformation💔 | IIT Motivation|Jee 2023 #transformation #iit #viral...
Beauty of the Brain😍 IQ - IIT Bombay
John G. Williamson & Martin van der Mark moebius light=Alain Connes=de Broglie Law of Phase Harm...
Bragg-Gleichung / Bragg-Bedingung
Albert Einstein doing physics | very rare video footage #shorts
IIT Bombay Lecture Hall | IIT Bombay Motivation | #shorts #ytshorts #iit
Комментарии
 0:08:12
0:08:12
 0:01:43
0:01:43
 0:06:18
0:06:18
 0:07:04
0:07:04
 0:03:09
0:03:09
 0:04:02
0:04:02
 0:00:48
0:00:48
 0:22:30
0:22:30
 0:16:29
0:16:29
 0:00:44
0:00:44
 0:22:10
0:22:10
 0:07:01
0:07:01
 0:06:16
0:06:16
 0:00:26
0:00:26
 0:00:58
0:00:58
 0:00:20
0:00:20
 0:00:20
0:00:20
 0:00:57
0:00:57
 0:00:20
0:00:20
 0:00:19
0:00:19
 0:01:51
0:01:51
 0:05:20
0:05:20
 0:00:13
0:00:13
 0:00:12
0:00:12