filmov
tv
Interval notation for where functions Increase, Decrease, Constant

Показать описание
Learn how to write Interval notation for where functions Increase, Decrease, and are constant in this free math video tutorial by Mario's Math Tutoring.
0:21 Example 1 Finding Where the Graph Increases, Decreases, Constant
0:53 Explanation of Why We Use Open Intervals
1:34 Hint on Using the X Values Not the Y Values
2:32 Example 2
Related Videos:
Interval Notation vs. Inequality Notation
Looking to raise your math score on the ACT and new SAT?
Check out my Huge ACT Math Video Course and my Huge SAT Math Video Course for sale at
For online 1-to-1 tutoring or more information about me see my website at:
* Organized List of My Video Lessons to Help You Raise Your Scores & Pass Your Class. Videos Arranged by Math Subject as well as by Chapter/Topic. (Bookmark the Link Below)
0:21 Example 1 Finding Where the Graph Increases, Decreases, Constant
0:53 Explanation of Why We Use Open Intervals
1:34 Hint on Using the X Values Not the Y Values
2:32 Example 2
Related Videos:
Interval Notation vs. Inequality Notation
Looking to raise your math score on the ACT and new SAT?
Check out my Huge ACT Math Video Course and my Huge SAT Math Video Course for sale at
For online 1-to-1 tutoring or more information about me see my website at:
* Organized List of My Video Lessons to Help You Raise Your Scores & Pass Your Class. Videos Arranged by Math Subject as well as by Chapter/Topic. (Bookmark the Link Below)
Interval Notation
Interval notation for where functions Increase, Decrease, Constant
Interval Notation Explained - The Basics You NEED to Know!
Write the domain in interval notation of a rational function
Intervals and interval notation | Functions | Algebra I | Khan Academy
How To Find The Domain of a Function - Radicals, Fractions & Square Roots - Interval Notation
How to determine the intervals that a function is increasing decreasing or constant
Graphing Interval Notation
This Integral Went Viral in USA | Integral xfloor(1/x)dx
Interval Notation (1 of 2: Bounded intervals)
Interval Notation for Increasing/Decreasing Functions
Find the Domain of Each Function Using Interval Notation: f(x) = x/x PLUS 2 MORE EXAMPLES!
Find the domain and write in interval notation of a square root function
Introduction to increasing, decreasing, positive or negative intervals | Algebra I | Khan Academy
Finding the Domain and Range From a Graph (Interval Notation)
Introduction to Interval Notation (Closed and Open)
Interval Notation Explained
How to Find the Domain of Any Function in Interval Notation: Rational & Exponential | T2 #1-4
Interval Notation to Set-Builder Notation | Pre-Calculus
Domain and Range Interval Notation
Increasing and Decreasing Functions - Calculus
How to Find the Domain and Range of a Graph Using Interval Notation
Interval Notation 📚 #Shorts #math #maths #mathematics #education #learn #learning
How to Find the Domain and Range of a Graph in Interval Notation
Комментарии
 0:10:51
0:10:51
 0:03:50
0:03:50
 0:08:41
0:08:41
 0:02:38
0:02:38
 0:09:35
0:09:35
 0:18:45
0:18:45
 0:02:56
0:02:56
 0:00:17
0:00:17
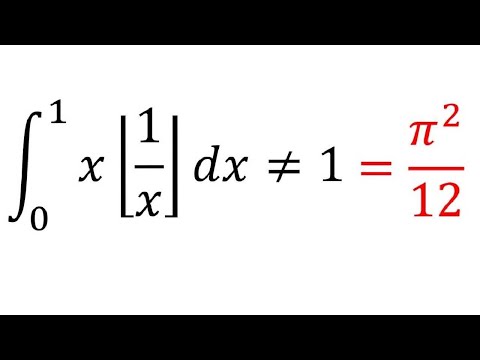 0:14:01
0:14:01
 0:11:20
0:11:20
 0:06:03
0:06:03
 0:11:32
0:11:32
 0:02:32
0:02:32
 0:05:55
0:05:55
 0:05:53
0:05:53
 0:05:14
0:05:14
 0:02:14
0:02:14
 0:06:56
0:06:56
 0:10:26
0:10:26
 0:26:32
0:26:32
 0:11:08
0:11:08
 0:03:59
0:03:59
 0:00:22
0:00:22
 0:06:16
0:06:16