filmov
tv
Olympiad Math | Solve Advance Algebric Expression in Simple Way
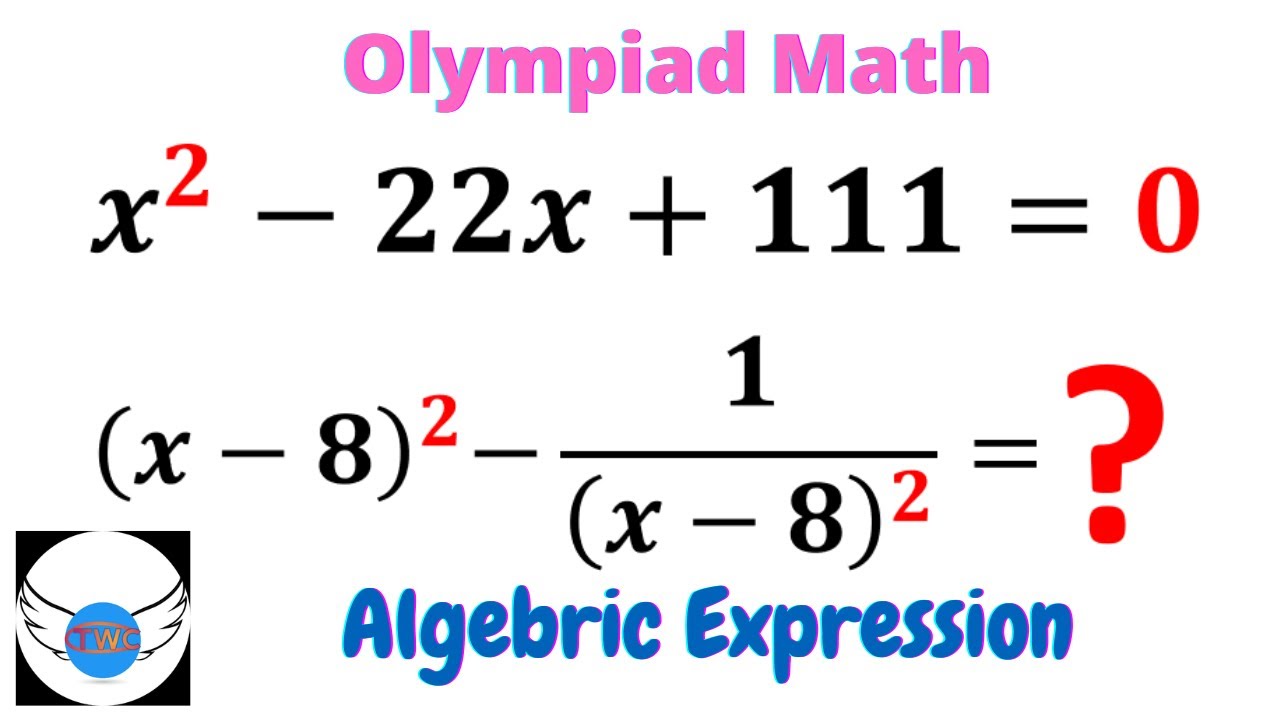
Показать описание
Olympiad Math | Solve Advance Algebric Expression in Simple Way
Hi Friends,
Today I will teach you tips and tricks to solve the given olympiad math question in a simple and easy method.
Learn how to solve the Olympiad Question quickly with my tips and tricks.
Olympiad Exam
math olympics
olympiad exam
olympiad exam sample papers
math olympiad sample questions
math olympiada
British Math Olympiad
olympics math
olympics mathematics
olympics math activities
olympics math competition
Math Olympiad Training
mathcounts
math at work
exponential equation
system of equations
solve system of equations
solve the equation
Linear Equation
Radical Equation
Learn how to solve Olympiad Question quickly
Olympiad Mathematics
Po Shen Loh
pre
problems of class 10
problems of class 9
Standard 10 math
Standard 10 Algebra
Math for Everyone
Easy understanding Method
Math for Weak student
Quadratic Equation ssc
Quadratic Equation bank clerk mains
Quadratic Equation cgl
Thanks,
The Warrior Classes
#algebricexpression
#olympiad
#Math_problem
Hi Friends,
Today I will teach you tips and tricks to solve the given olympiad math question in a simple and easy method.
Learn how to solve the Olympiad Question quickly with my tips and tricks.
Olympiad Exam
math olympics
olympiad exam
olympiad exam sample papers
math olympiad sample questions
math olympiada
British Math Olympiad
olympics math
olympics mathematics
olympics math activities
olympics math competition
Math Olympiad Training
mathcounts
math at work
exponential equation
system of equations
solve system of equations
solve the equation
Linear Equation
Radical Equation
Learn how to solve Olympiad Question quickly
Olympiad Mathematics
Po Shen Loh
pre
problems of class 10
problems of class 9
Standard 10 math
Standard 10 Algebra
Math for Everyone
Easy understanding Method
Math for Weak student
Quadratic Equation ssc
Quadratic Equation bank clerk mains
Quadratic Equation cgl
Thanks,
The Warrior Classes
#algebricexpression
#olympiad
#Math_problem
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
Olympiad Math 3|Solve Advance Algebraic Equations #algebra #olympiad
Olympiad Math|SolveAdvance AlgebraicEquations#algebra #olympiad
A beautiful international math olympiad problem
United States l can you solve?? l Olympiad Math
Norway Math Olympiad Question | You should be able to solve this!
Germany l| Can you solve this?? l Olympiad Math exponential problem✍️🖊️💯
Olympiad Math Problem 3|Solve Advance Algebraic Equations#algebra #olympiad
Olympiad Math | Solve Advance Algebric Expression in Simple Way
Advanced Olympiad Mathematics Question
Luxembourg - Math Olympiad Question | You should know this trick
A Nice Math Olympiad Exponential Equation 3^x = X^9
Russian l Very Nice Olympiad Math Exponential Problem l find value of k?
A difficult olympiad math problem | China Math Olympiad Questions
A Nice Olympiad Algebraic Equation • x/y+y/x=? #shorts #olympiad #mathematics #matholympiad #maths
New Zealand - Math olympiad Question
Math Olympiad Question | Equation solving | You should learn this trick to pass the exam
IITian Inside: Math Olympiad Toughest Question ka OP Solution #jee1
Math Olympiad Question | Indices - Equation Solving | A Must Known Trick
A Nice Algebraic Radical Problem #shorts #olympiad #maths #mathematics #tips #matholympiad #algebra
A nice olympiad exponential problem #short #olympiad #mathematics #maths #exponents #trending
A Nice Math Olympiad Algebraic Expansions Problem. #math #olympiad #mathematics #matholympiad #viral
The Hardest Math Test
A Nice Exponents Olympiad Problem • X=?¿ #shorts #olympiad #mathematics #matholympiad #maths #tips...
Комментарии
 0:00:52
0:00:52
 0:08:43
0:08:43
 0:10:05
0:10:05
 0:01:00
0:01:00
 0:09:16
0:09:16
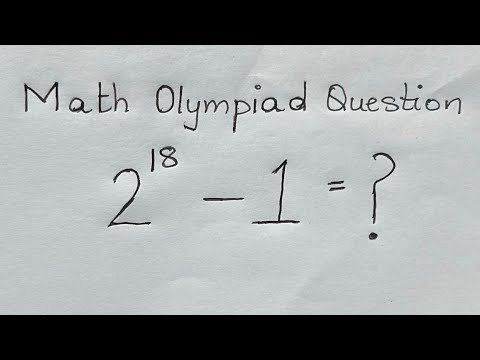 0:03:21
0:03:21
 0:16:32
0:16:32
 0:08:12
0:08:12
 0:06:45
0:06:45
 0:08:30
0:08:30
 0:02:51
0:02:51
 0:02:34
0:02:34
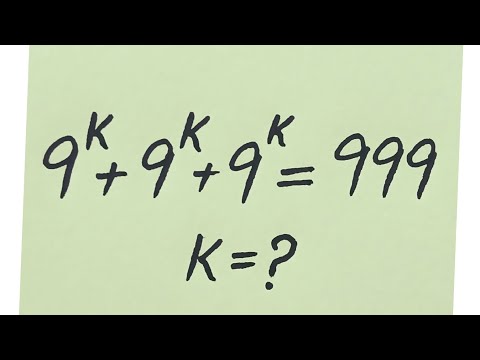 0:09:27
0:09:27
 0:09:20
0:09:20
 0:00:53
0:00:53
 0:01:12
0:01:12
 0:01:54
0:01:54
 0:00:39
0:00:39
 0:02:44
0:02:44
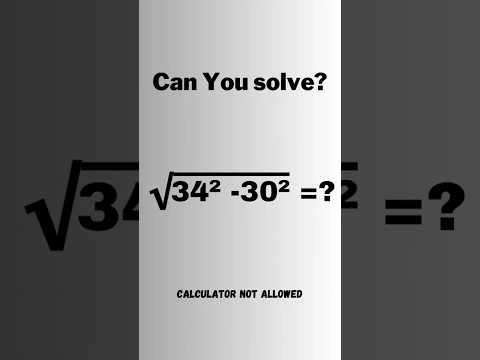 0:00:44
0:00:44
 0:00:35
0:00:35
 0:00:51
0:00:51
 0:00:28
0:00:28
 0:00:45
0:00:45