Product of chords?

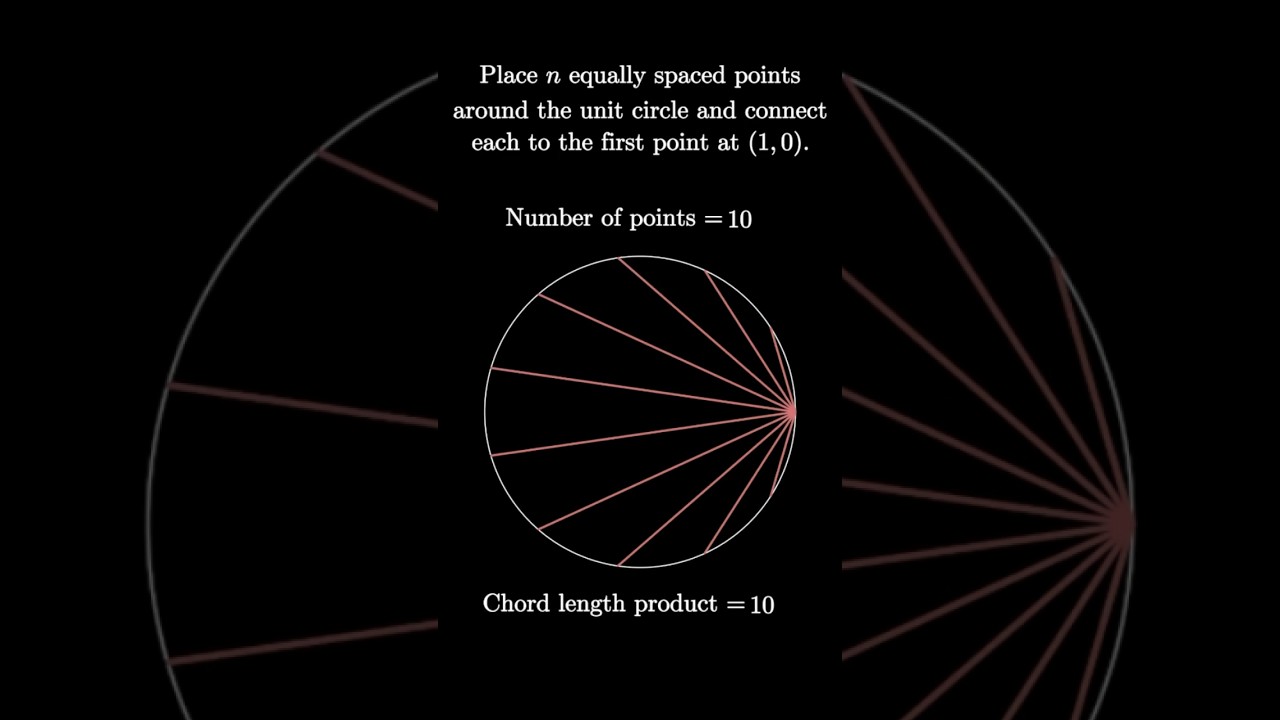
This short animation shows chords connecting n equally space points to one of those points on a unit circle and computes the product of the chord lengths. Do you have a conjecture based on this? Can you prove it?

#math #mathvideo #manim #circle #chords #visualproof #trigonometry #sine #cosine #tangent #rootsofunity #complexanalysis #complexnumbers #products #geometry

[muffinmainia]

I’d love to see an explanation/proof for this!

[brendankoelsch]

The Chanel name covers it, but for anyone who’s wondering the bottom number says “chord length product”

[quantumbuddha]

Wow! Very cool! I was not aware of this property of chords.

[catmacopter]

I wonder if there is a proof for this using roots of unity! Each chord would have length of abs(1-[root]).

[nintendoswitchfan]

It can be proved by thinking of the circle as the complex unit circle and the chord lengths are the absolute value of a difference of complex numbers

[rcb]

Man, I was watching this short at a such a scale that the links and info at the bottom obscured the part of the video that reads "Chord length product = ..." and watched the thing for 3 loops wondering what the hell I was missing.

[vennstudios]

Wait so
4 points has
2×(√2)² soo maybe which us 4 chords

So if we back track

The chord would be a triangle with a base of 1+|cos120| or 3/2 and a height of √3/2 so Pythagorean theorem it comes out as 9/4+3/4 which comes down to 3sq
Then √3

Then realization kicks in

I'm not smart enough to conclude anything with this

Google is my trusted navigator