filmov
tv
Master Condensing Logarithmic Expressions using the Properties of Logarithms

Показать описание
And what I did is I wrote the expanded form of a logarithm. And then I wrote what the equivalent expression for that is in the condensed format. So you can see I have one example here, another logarithm here, another example there.
So I kind of ran out a little bit, got tight on space. But I put each logarithm. So this would be basically your product property, your quotient property, and here it'd be basically your power property.
And in another video, I explain how those kind of relate. And they're similar to the rules of exponents and so forth. But the main important thing, the really kind of idea, and we're going to use all of these properties here-- and what we're trying to do is we're trying to condense our logarithmic expression. You can see that these expressions are separated by addition and subtraction.
And what we're going to do is we want to condense these into one single logarithmic expression. So to do that, first of all, if you can see here, by using my addition property, when I have two logarithms separated by addition, I can condense them into the product of our two values of the logarithms, x and y.
So in this case, I have log base 4 of 20 plus log base 4 of 3. Well, therefore, that's going to equal log base 4 of 20 times 3. Now, for some of these, I'll break them out step by step. And some of these I'm going to run out of a little bit of a space, as well.
However, that can simplify now to the log base 4 of 60. Now, we always want to see if we can simplify this a little bit further. Some of these I chose, we will be able to simplify. Some you will not.
We know that 4 raised to the third power is 64. But I can't really simplify this any other further to be able to evaluate. So I'm just going to leave it as log base 4 of 60.
In the next problem here, now you can see we have division. So to do this next problem, when you have terms of logarithms separated by addition, you can rewrite them as the product. So when you have terms separated by subtraction, we can rewrite them as the quotient of one single logarithm.
So this would be log base 2 of 18 divided by 3. Well, 18 divided by 3 is going to be 6. So therefore, I can rewrite this as log base 2 of 6. And again, that's not something I can simplify because 2 doesn't raise to a given power to give me 6. So therefore, I'm just going to leave my answer as is.
So hopefully, ladies and gentlemen, you just kind of get an idea of what we're doing. The main important thing is taking these expressions and condensing them down to one logarithmic expression.
So now I'm going to start incorporating another rule. And that other rule is the power rule. And what the power rule basically states is if you have a value that's being multiplied by your logarithm, in front of it, you can basically rewrite that as your power of your logarithm.
So in this case, what I'm going to do is I'm going to apply that power rule for each of my powers. So therefore, I have log of x squared plus log of y cubed plus log of z to the fourth. Now, also notice that the logarithms do not have a base in this case. My logarithms does not have a case.
But fear not. When your logarithms does not have a base-- oh, I forgot something. That's supposed to be x plus. This is supposed to be 2x minus. Let's do it like that. There you go.
So when they don't have a base, just remember if your logarithm doesn't have a base, then we can assume it's base 10. Now, that's not really going to affect our condensing. But it is important we can only apply these rules when the base is exactly the same. So I didn't do any examples here because there's really not much to do for it.
But if you have a logarithmic expression that you're trying to condense and the bases are different-- for instance, if I had like 5 and 10 or something, or 5 and 2-- you couldn't follow these rules of order of operations. So if there's not a base given, we assume that it's going to be 10.
Well, now I have addition and I have addition. So I can rewrite this as one single logarithm, as the product of my three values. So therefore, I just write this as log of-- I always write this. I don't need parenthesis-- x squared, y cubed, z to the fourth.
Now, I forgot to write this one in. But in the next example, now we have natural logarithm, ln. And natural logarithm is the same thing. I don't have any room here.
Well, I guess I can write here. So log base a of x is the same thing as ln of x. And basically what that means is ln of x just tells us that it's going to have a base e.
Комментарии
 0:13:09
0:13:09
 0:03:43
0:03:43
 0:03:54
0:03:54
 0:01:53
0:01:53
 0:02:25
0:02:25
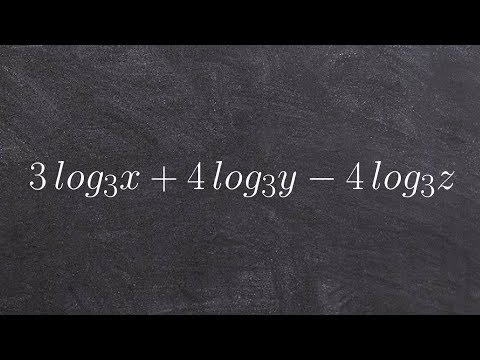 0:01:22
0:01:22
 0:03:21
0:03:21
 0:02:51
0:02:51
 0:01:53
0:01:53
 0:01:00
0:01:00
 0:04:01
0:04:01
 0:04:36
0:04:36
 0:02:00
0:02:00
 0:01:53
0:01:53
 0:10:20
0:10:20
 0:01:11
0:01:11
 0:01:36
0:01:36
 0:01:30
0:01:30
 0:11:40
0:11:40
 0:09:34
0:09:34
 0:01:00
0:01:00
 0:03:22
0:03:22
 0:04:29
0:04:29
 0:01:14
0:01:14