Introduction to Bayesian statistics, part 1: The basic concepts

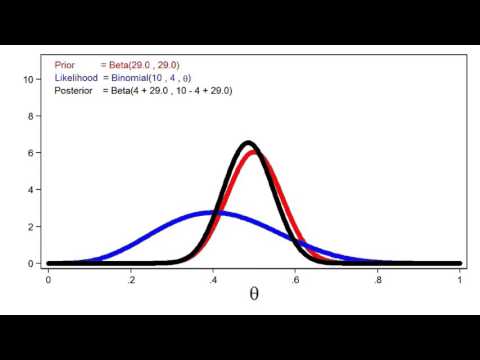
An introduction to the concepts of Bayesian analysis using Stata 14. We use a coin toss experiment to demonstrate the idea of prior probability, likelihood functions, posterior probabilities, posterior means and probabilities and credible intervals.

Copyright 2011-2019 StataCorp LLC. All rights reserved.

[vietta]

Wow, my understanding acquired from this video is more than from dozen of hours on classes.

[ahmedmoneim]

That was excellent explanation of the interaction between the parameters, thank a lot for putting the time and effort to do the animations

[SuperDayv]

This is the best introduction to this that I've found online! Thanks!

[AradAshrafi]

It was the most comprehensive video with the amazing explanations about prior, likelihood, and posterior. Thank you so much for this wonderful video.

[jehangonsal]

This is awesome. So intuitive and interesting. Why did we ever use null hypothesis testing? With the computational power we have now, this should be the norm.

[pep__climate]

What to say, an excellent explanation of Bayesian updating, long life to Stata and its People!

[ngm_]

Your teaching style is very effective. Explanation and pacing is very good and your voice maintains attention very well. Thank you for making this video, it was quite informative.

[divyateja]

excellent explanation. I had been surfing internet, for clarity

[SoumyadeepMisra]

Thank you Sir, the best explanation I found on youtube..

[emilyzheng]

Thank you very much for the explanations of non-informative prior and informative prior. Very helpful for my research.

[jennyapl]

Posterior is proportional to the MLE x prior, not equal =

[MA-rceo]

Thank you for making this video. I took statistics class before, but my knowledge is limited. Please add descriptive details so I can understand your video.

[bigfishartwire]

Finally I understand this thing. Thank you.

[lostcaze]

Thank you. The first video that makes me understand this reasoning in one go.

[nyambaatarbatbayar]

I have the same version of Stata as yours. However, my Bayesmh window doesn't have the "univariate distribution" option. What could be the reason? Can you give me a hint?

[alexisdasiukevich]

How is it that you are able to neglect the probability of y for the posterior distribution function, which is normally on the denominator?

[chilliandspiceandallthings]

Maybe the video creator intended to explain Bayesian statistics, but did not.

The concepts start to be explained, then there is a stepwise jump into mentioning prior and posterior probability, with the introduction of on screen equations but no further explanations - it's like it was read out of a technical manual that only 'insiders' know about. This then quickly turns into how to use the software/which buttons to press, which seems applicable to those who already know about Bayes and want to use the software - and not for those who want an introduction.


So I'm sorry to say this video was not useful to introduce Bayesian statistics and I would recommend giving it a miss.

[shreyaskrishna]

What i dont understand is how is multiplying liklihood and prior distribution going to give us what we call the posterior distribution. If anything the product just seems like a random function

[sukursukur]

How can we specify belief power of prior? In this example alfa, beta=30. And we can assign 250 for both. There is no boundary for us to prevent assigning 250 instead of 30. In a real life data, if you assign powerful prior, this means you have a bias and you may have implemented pressure to information coming from data; otherwise you have come close to non-prior case.

[kathyern]

If the coin is held with heads facing up, what is the likelihood it will yield heads when it is tossed?
If the con is held with heads facing up, what is the likelihood it will yield tails when it is tossed?
If the coin is held with tails facing up, what is the likelihood it will yield tails when it is tossed?
If the coin is held with tails facing up, what is the likelihood it will yield heads when it is tossed?