filmov
tv
Example 3: Solving systems by substitution | Systems of equations | 8th grade | Khan Academy

Показать описание
Solving systems by substitution 3
Missed the previous lesson?
8th grade on Khan Academy: 8th grade is all about tackling the meat of algebra and getting exposure to some of the foundational concepts in geometry. If you get this stuff (and you should because you're incredibly persistent), the rest of your life will be easy. Okay, maybe not your whole life, but at least your mathematical life. Seriously, if you really get the equations and functions stuff we cover here, most of high school will feel intuitive, even relaxing. (Content was selected for this grade level based on a typical curriculum in the United States.)
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to Khan Academy’s 8th grade channel:
Комментарии
 0:04:58
0:04:58
 0:06:04
0:06:04
 0:05:08
0:05:08
 0:02:38
0:02:38
 0:12:44
0:12:44
 0:10:27
0:10:27
 0:05:10
0:05:10
 0:04:08
0:04:08
 0:09:24
0:09:24
 0:05:15
0:05:15
 0:12:45
0:12:45
 0:09:39
0:09:39
 0:06:47
0:06:47
 0:06:08
0:06:08
 0:09:53
0:09:53
 0:10:21
0:10:21
 0:10:52
0:10:52
 0:08:25
0:08:25
 0:36:45
0:36:45
 0:03:47
0:03:47
 0:08:51
0:08:51
 0:02:19
0:02:19
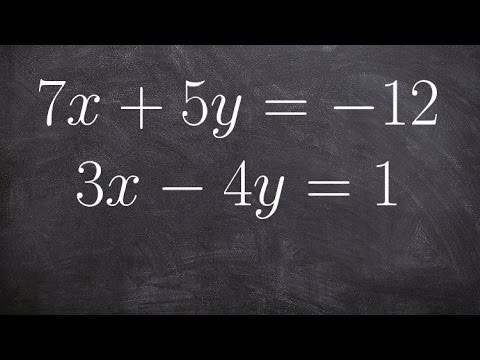 0:04:34
0:04:34
 0:01:54
0:01:54