How Row Operations Change the Determinant | Linear Algebra

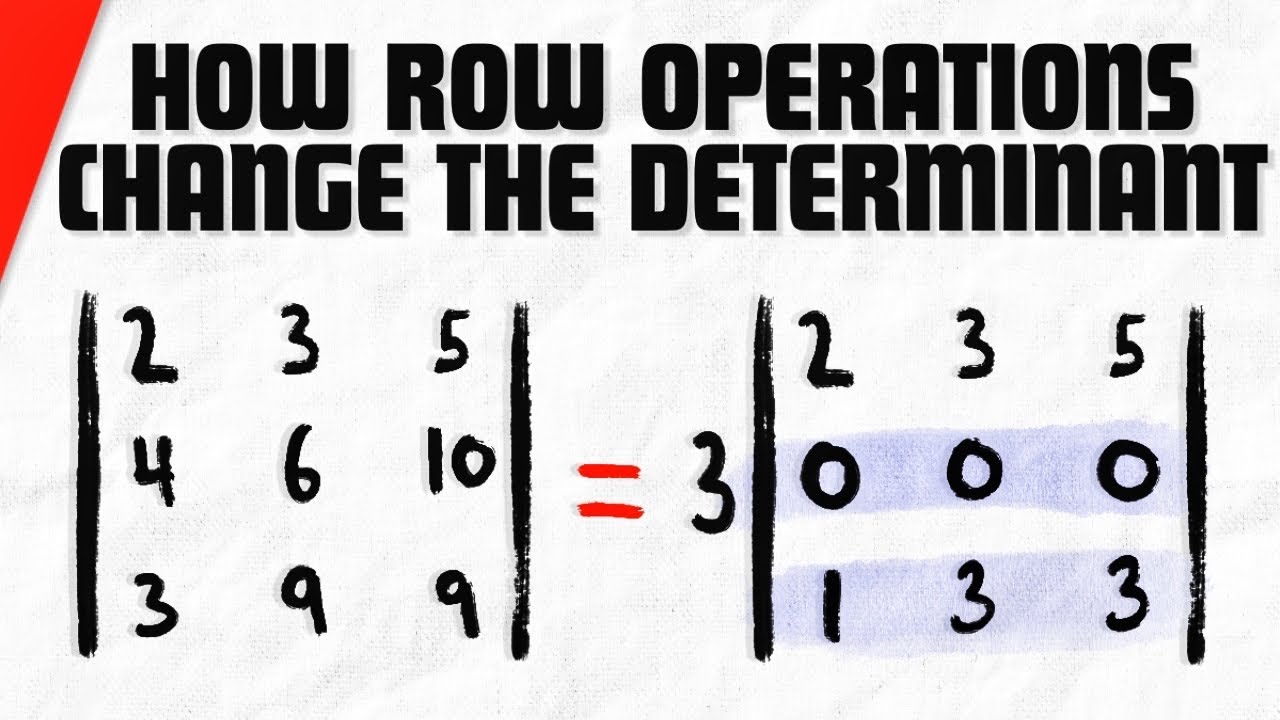
We see how performing elementary row operations on a matrix changes the determinant. Using this knowledge, we can easily find the determinants of elementary matrices. We go over the fact that a matrix with proportional rows or columns has a determinant of 0, and we see how to find the determinant using row reduction. #linearalgebra

Join Wrath of Math to get exclusive videos, music, and more:

0:00 Intro
0:29 The Effects of Elementary Row Operations
4:10 Determinants of Elementary Matrices
6:10 Proportional Rows Implies Determinant 0
7:22 Finding Matrix Determinant by Row Reduction

◉Textbooks I Like◉

★DONATE★

Thanks to Loke Tan, Raül Beienheimer, Matt Venia, Micheline, Doug Walker, Odd Hultberg, Marc, Shlome Ashkenazi, Barbora Sharrock, Mohamad Nossier, Rolf Waefler, Shadow Master, and James Mead for their generous support on Patreon!

Outro music is mine. You cannot find it anywhere, for now.

Follow Wrath of Math on...

[PunmasterSTP]

It still seems odd to me that adding one row to another doesn't change the value of the determinant, especially adding multiples of one row to another. I understand the proof and everything, it's just kind of interesting to think about...