filmov
tv
Derivative equals inverse

Показать описание
In this video, I find a function whose derivative equals to its inverse function. The answer is quite surprising!
Derivative equals inverse
A fascinating differential equation: when the derivative equals the inverse function
nth derivative equals inverse
Derivatives of inverse functions | Advanced derivatives | AP Calculus AB | Khan Academy
Finding the Derivative of an Inverse Function - Calculus I
Proof that derivatives and integrals are inverse operators geometrically
Derivatives of Inverse Functions | Calculus
Evaluate the derivative of the inverse function
The Derivative Inverse Functions
A fascinating differential equation: when the 2nd derivative equals the inverse function
Derivative of inverse function given an equation
Derivatives of Inverse Functions
Derivative of Inverse Functions | Calculus 1
Derivatives of Inverse Functions | This is how You Rock Calculus!
Derivatives of inverse functions: from equation | AP Calculus AB | Khan Academy
Determine a Derivative Function Value and a Derivative Value of an Inverse Function (Linear)
derivative of inverse secant
Derivatives of Inverse Trigonometric Functions
Finding the Derivative of An Inverse Function | Quintics
Find the Derivative of an Inverse Function with the Chain Rule in Calculus
KutaSoftware: Calculus- Derivatives Of Inverse Functions
Derivative of Inverse Function: Proof with Limits
Derivative of an Inverse Function (for AP Calculus!)
Find the derivative inverse function given a point
Комментарии
 0:12:35
0:12:35
 0:09:12
0:09:12
 0:14:53
0:14:53
 0:04:46
0:04:46
 0:05:33
0:05:33
 0:08:16
0:08:16
 0:13:31
0:13:31
 0:03:07
0:03:07
 0:51:36
0:51:36
 0:09:22
0:09:22
 0:03:19
0:03:19
 0:12:23
0:12:23
 0:06:40
0:06:40
 0:05:26
0:05:26
 0:05:03
0:05:03
 0:05:47
0:05:47
 0:04:42
0:04:42
 0:06:19
0:06:19
 0:08:32
0:08:32
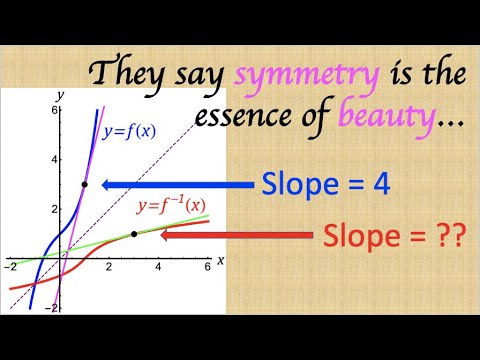 0:09:30
0:09:30
 0:20:14
0:20:14
 0:05:06
0:05:06
 0:14:31
0:14:31
 0:00:55
0:00:55