filmov
tv
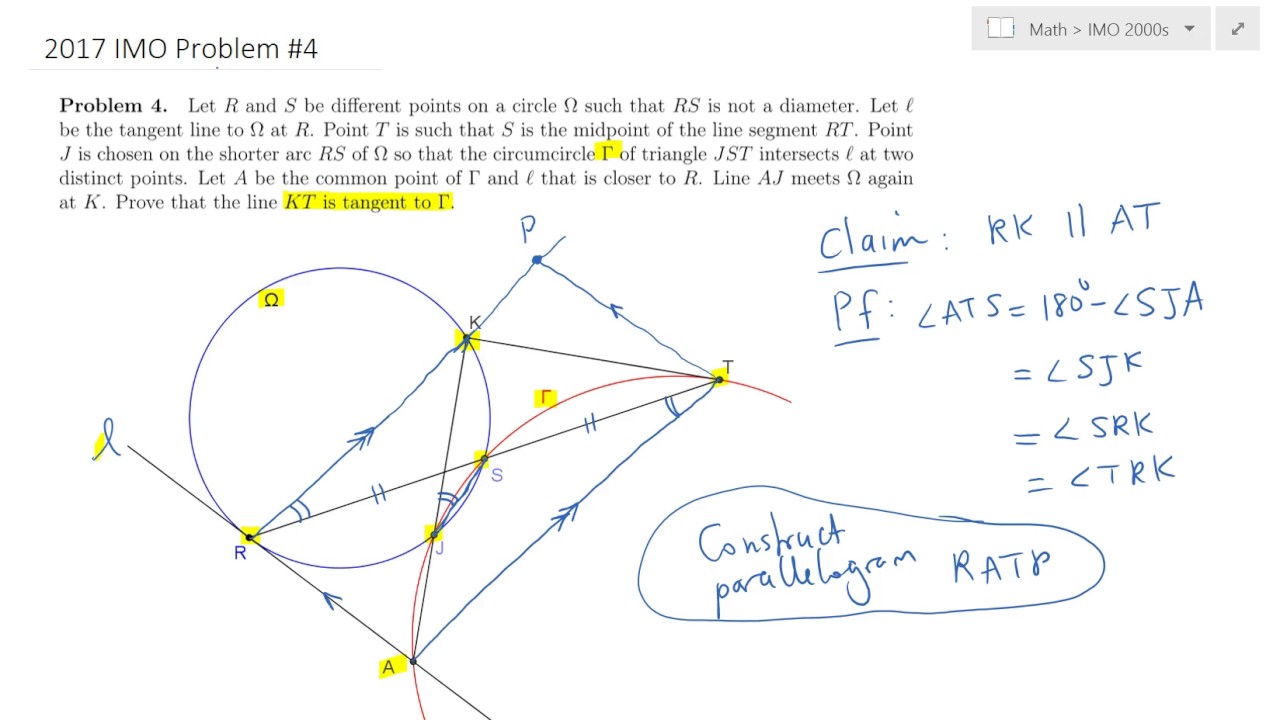
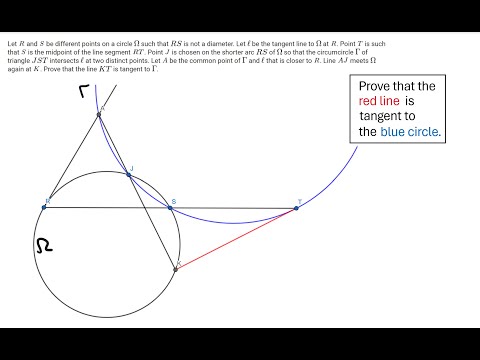
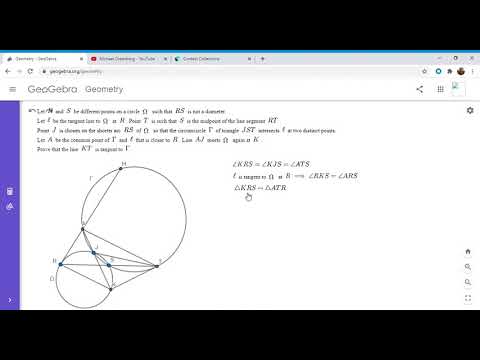
2017 IMO Problem #4
Показать описание
2017 IMO Problem #4
2017 IMO Problem 4
2017 IMO Problem 4
IMO 2017 Problem 4: Solving IMO Geometry in 3 minutes
The FIRST Ever IMO Problem
Olympiad Geometry Problem #43: IMO 2017 #4
Chinese IMO team
2018 IMO problem 4 || This one is hard!
2021 IMO Problem 4 Solution: Quadrilateral with equal perimeter?
2018 IMO Problem 4 Solution
Olympiad Geometry Problem #67: IMO Shortlist 2017 G4
2021 IMO Problem 1 Solution: Cards sums to Perfect Square
2018 IMO Problem 5 Solution
Solve an IMO problem in 5 minutes (1975 Problem 4)
2017 IMO Problem #5
International Math Olympiad, IMO 1961, Problem 3, Solve The Equation
58th International Mathematical Olympiad (IMO 2017)
Cracking the Code Unveiling the Infinite Series of √4 #IMO #InfiniteSeries #Maths #RootOf4 #olympiad...
Geometry question to test the world's best math students (IMO 2024 problem 4)
IMO 2022 Problem 4
The unexpectedly hard windmill question (2011 IMO, Q2)
Imo Notification Settings | Imo App Notification Settings | #shorts
2014 IMO Problem #4
NICEST IMO Problem Ever? Ninja Says Yes! (IMO 2023 P5) #SoME3
Комментарии
 0:07:48
0:07:48
 0:08:06
0:08:06
 0:04:42
0:04:42
 0:03:01
0:03:01
 0:00:40
0:00:40
 0:08:42
0:08:42
 0:00:34
0:00:34
 0:10:44
0:10:44
 0:03:29
0:03:29
 0:07:00
0:07:00
 0:13:23
0:13:23
 0:05:17
0:05:17
 0:12:10
0:12:10
 0:04:56
0:04:56
 0:19:35
0:19:35
 0:14:45
0:14:45
 0:04:46
0:04:46
 0:00:36
0:00:36
 0:20:28
0:20:28
 0:23:38
0:23:38
 0:16:03
0:16:03
 0:00:25
0:00:25
 0:14:49
0:14:49
 0:09:52
0:09:52