filmov
tv
The Differential Operator (1 of 2: Introduction to notation)

Показать описание
The Differential Operator (1 of 2: Introduction to notation)
Differential equations, a tourist's guide | DE1
Using Differential Operators
Linear Differential Operators: Introduction
🔵24 - D Operator Method for Solving First Order Linear Differential Equations
ECE 201 Online Class - Differential Operators
Find a Linear Differential Operator that Annihilates the Function 1 + 7e^(2x)
4.4 Solve a System with the Differential Operator, Differential Equations
Fixed Point Iteration Method (Application). How iteration function accept for convergence.
But what is a partial differential equation? | DE2
Differential operators
Difference Between Partial and Total Derivative
Find a Linear Differential Operator that Annihilates 1 + 6x - 2x^3
Find a Linear Differential Operator that Annihilates the Function x^3(1 - 5x)
🔵25 - D Operator Method for Solving Second Order Linear Differential Equations
The Differential Operator and Exponential Shift
Verify that (xD + 1)(D - 2)y != (D - 2)(xD + 1)y where D is the Differential Operator
Solving second order differential equation using operator D
a7 1 10 Eigenvectors of the differential operator
Differential equations : - ( Differential and inverse differential operator ) - 43.
Find a Linear Differential Operator that Annihilates e^(-x)sin(x) - e^(2x)cos(x)
D-Notation and Determine a Linear Differential Operator of a Linear Differential Equation
Differential Equations: Method of Undetermined Coefficients - Annihilator Approach
Differential Operator Notation
Комментарии
 0:27:16
0:27:16
 0:10:35
0:10:35
 0:06:27
0:06:27
 0:39:06
0:39:06
 0:50:27
0:50:27
 0:02:19
0:02:19
 0:06:18
0:06:18
 0:04:03
0:04:03
 0:17:39
0:17:39
 0:17:03
0:17:03
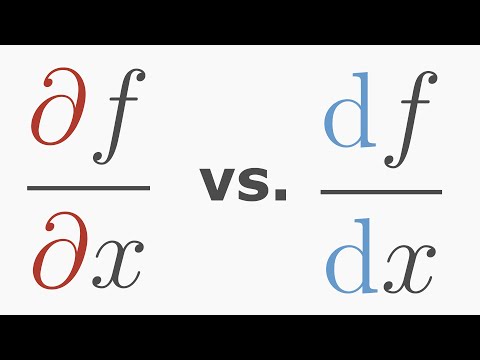 0:01:44
0:01:44
 0:02:06
0:02:06
 0:02:39
0:02:39
 0:18:39
0:18:39
 0:15:05
0:15:05
 0:06:06
0:06:06
 0:17:39
0:17:39
 0:04:54
0:04:54
 0:04:26
0:04:26
 0:02:11
0:02:11
 0:05:12
0:05:12
 0:26:22
0:26:22
 0:06:08
0:06:08