filmov
tv
Solve trig equations with exact solutions - the easy way (unit circle)

Показать описание
A simple way to visualise trigonometric equations lets us solve them quickly using spatial intuition. No need for CAST or ASTC (all stations to central/all students take calculus) mnemonics. I remember Dr Hoffman saying "This is how trigonometry should be taught in schools" before he showed us these techniques.
In this video I'll just be covering simple trig equations with exact solutions, for both degrees and radians. For example, equations like sin theta = -1/2, cos theta = sqrt(2)/2, tan theta = -sqrt(3), sin theta = -sqrt(3)/2, cos theta = 1/2, tan theta = -1, and sin theta = 0. And I'll show you how to work with radians so you can find angles like 11pi/6 or 5pi/4 on the unit circle.
In this video I'll just be covering simple trig equations with exact solutions, for both degrees and radians. For example, equations like sin theta = -1/2, cos theta = sqrt(2)/2, tan theta = -sqrt(3), sin theta = -sqrt(3)/2, cos theta = 1/2, tan theta = -1, and sin theta = 0. And I'll show you how to work with radians so you can find angles like 11pi/6 or 5pi/4 on the unit circle.
Solve trig equations with exact solutions - the easy way (unit circle)
Find the solutions to a trig equation between 0 and 2pi
Ex: Solve a Factorable Trig Equation Using Radians - Exact Solutions
How To Solve Trigonometric Equations With Multiple Angles - Trigonometry
Ex: Solve a Factorable Trig Equation with Exact and Rounded Radian Solutions
Solving Trigonometric Equations By Finding All Solutions
Ex: Solve a Factorable Trig Equation Requiring Substitution Using Radians - Exact Solutions
Solving Trig Equations (General Solution and [0,2pi))
Solving Trigonometric Equations - How to Write General Solution
Trigonometric Equation Exact Solution Sine Q1
Solving Trigonometric Equations | A-level Mathematics
Solving Trigonometric Equations (1 of 5: Overview)
Lesson 3 Solving trig equations in Radians using CAST
A2 Maths - Pure - Solving Trig Equations in Radians Mode
Solve Trigonometric Equations without a Calculator
How to Solve Trigonometric Equations (Precalculus - Trigonometry 22)
Trigonometry lesson 16 - Solving trigonometric equations using exact values
Solving a trigonometric equation by factoring
How to find all the solutions to a trigonometric equation
How To Find The Exact Values of Trig Functions
determine all of the solutions between 0 and pi for a trigonometric eqn using factoring
Solving trigonometric equations that use non-Unit Circle Values
An Introduction to Solving Trigonometric Equations
Exact Values (2 of 4: Solving a basic trigonometric equation)
Комментарии
 0:15:18
0:15:18
 0:03:38
0:03:38
 0:04:06
0:04:06
 0:11:34
0:11:34
 0:05:34
0:05:34
 0:11:49
0:11:49
 0:04:04
0:04:04
 0:19:05
0:19:05
 0:06:26
0:06:26
 0:09:31
0:09:31
 0:38:12
0:38:12
 0:06:38
0:06:38
 0:16:18
0:16:18
 0:13:57
0:13:57
 0:17:41
0:17:41
 1:34:36
1:34:36
 0:12:45
0:12:45
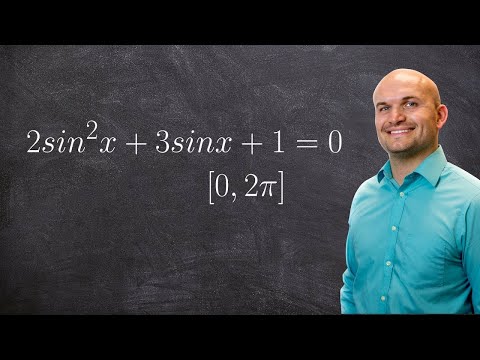 0:05:19
0:05:19
 0:08:40
0:08:40
 0:12:39
0:12:39
 0:05:41
0:05:41
 0:06:50
0:06:50
 0:14:17
0:14:17
 0:12:05
0:12:05