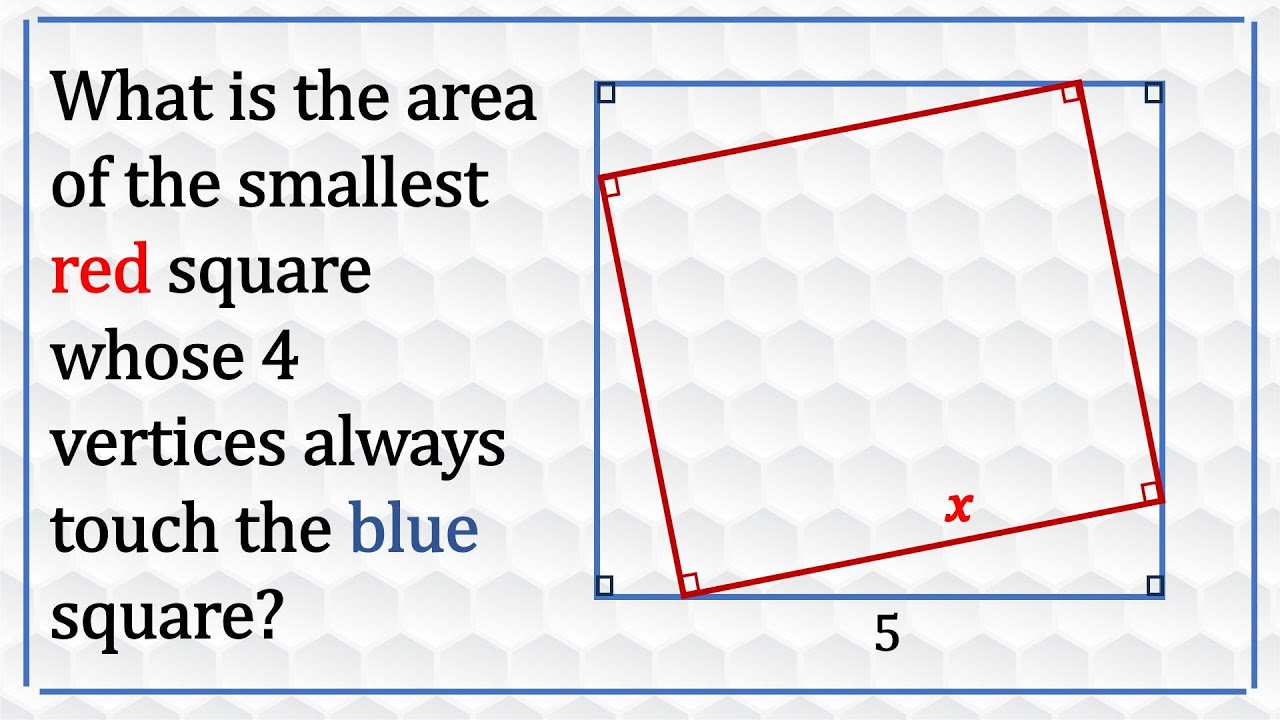
The smallest square inscribed in another square

In this video, I showed how to find the minimum area of an inscribed square in another square using the vertex form of the resulting quadratic

[albertpaquette]

You are a delightful teacher. If you could be cloned, mathematics would be a favourite topic in schools around the world.

[renesperb]

If you consider symmetry the answer is obvious : the corners have to be midpoints of the large square.Your approach is clear and well
presented .

[renesperb]

A suggestion, simplifying the calculation a little: if you take the distance t from the midpoint on the side of the large square (side s), the inscribed square has the
area (s/2 + t)^2 . This is increasing in t, hence t = 0 is optimal .

[eval_is_evil]

I love this, really like your calligraphy and also hello from Central Europe !

[punditgi]

Excellent lesson! Plus I love the hat! ❤🎉😊

[ZipplyZane]

Gonna put out my answer before watching. It appears to me that the answer will be 12.5. Why?

The largest width of a square is at its diagonal, and the shortest length is its side. Thus the smallest square inscribed in the larger square will need those two lengths to be the same. So now we have only to find the side length of the smaller square.

This can be done either by knowing the ratio of the diagonal to the side, or derived easily by noticing that a square can be divided into two congruent triangles (using the Side Angle Side theorem if you want to be specific). These are both right triangles and have two sides the same, meaning they are 45-45-90 triangles. From there you get that the hypotenuse is sqrt(2) times the side.

So now we know the side length or x = 5 / sqrt(2). The area, or x^2 will thus be 25/2, or 12.5.

----

Intuitively, I also noticed that the corners of the inner square would be on the midpoints of the outer square. Divide up the inner square with triangles, show they're the same size as the others, then notice you have 4/8 triangles, or 1/2 the outer area.

I'm just not quite sure how to justify that first statement. I know the diagonal of the middle square would need to be parallel with the outer square's edges to be able to reach, but not quite how to explain it.

[kamalhammoud]

I thought i would be the square of vertices that are midpoint, if you subtract area of square in terms of t by area of square such that t=2.5, then you get a function is greater than zero for all t different than 2.5
This implies that each area of all possible squares is greater than area of square of vertices that are midpoints
Then minimum area is 2×(2.5)^2=25/2

[anestismoutafidis]

5÷2^1/2=3, 5355<=> 3, 5355^2=12, 5

[masoudhabibi]

Thanks..please draw the following function y=(x^2+x_2)/(x^3_1)