filmov
tv
A circle with an inscribed square – can you find the area of the square?

Показать описание
Help with Middle and High School Math
Test Prep for High School Math, College Math, Teacher Certification Math and More!
Popular Math Courses:
Math Foundations
Math Skills Rebuilder Course:
Pre-Algebra
Algebra
Geometry
Algebra 2
Pre-Calculus
• MIDDLE & HIGH SCHOOL MATH
• HOMESCHOOL MATH
• COLLEGE MATH
• TEST PREP MATH
• TEACHER CERTIFICATION TEST MATH
A circle with an inscribed square – can you find the area of the square?
Given a Circle Inscribed in a Triangle, Find the Radius of the Circle.
EGD Inscribed Circle
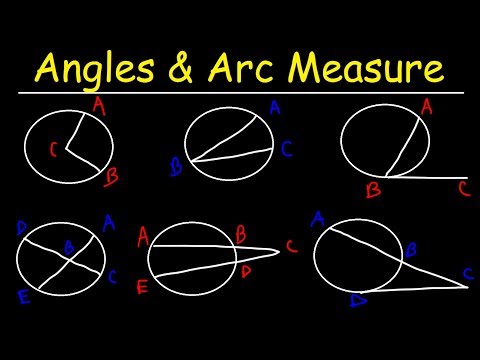
Circles, Angle Measures, Arcs, Central & Inscribed Angles, Tangents, Secants & Chords - Geom...
Can you find the Radius of the circle? | (Triangle inscribed in a circle) | #math #maths
Geometry! What is the radius of a circle inscribed in a circular sector??
A triangle is inscribed in a circle – what’s the radius?
Circles: Inscribed Angles, Intercepted Arcs
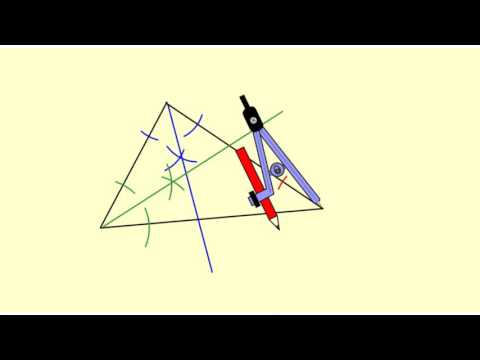
How to draw the Incenter and the Inscribed Circle of a triangle
Inscribed Circle in a Right Triangle | Daily Math Geometry
Circles: Inscribed Quadrilateral (Example Three)
A Circle Inscribed in a Triangle | Geometry | Math Video Central
Triangle inscribed in a circle | 3 Different Methods to Find the Radius of the Circle
finding the radius of a circle inscribed in a right triangle
Central Angles and Inscribed Angles
Can you find the area of the circle? | Triangle inscribed in a circle | (Math skills) | #math #maths
In-depth explanation! | Find Radius of the circle? | (Circle inscribed in a triangle) | #math #maths
A quarter circle with radius 4 cm has a circle inscribed in it as shown above. What is the diameter?
Find the Radius of inscribed circle using Area and sides of Triangle | Find the Radius of circle
A square is inscribed in a circle with radius = 5, what is the area of the square?
Inscribe a Circle in a Triangle
Geometry! What is the radius of a circle inscribed in a square??
Draw a Circle Inscribed in a Triangle #shorts
Radius of Inscribed Circle Theorem (Geometry #194)
Комментарии
 0:12:12
0:12:12
 0:04:31
0:04:31
 0:02:14
0:02:14
 0:32:31
0:32:31
 0:10:25
0:10:25
 0:04:59
0:04:59
 0:17:08
0:17:08
 0:04:40
0:04:40
 0:05:41
0:05:41
 0:03:51
0:03:51
 0:05:32
0:05:32
 0:03:41
0:03:41
 0:19:06
0:19:06
 0:04:06
0:04:06
 0:06:51
0:06:51
 0:08:49
0:08:49
 0:15:31
0:15:31
 0:01:36
0:01:36
 0:03:42
0:03:42
 0:15:17
0:15:17
 0:03:06
0:03:06
 0:03:27
0:03:27
 0:00:21
0:00:21
 0:02:17
0:02:17