Laplace Transform Visually Explained, Part 2: Unit Step (Piecewise), Exponential, & Cosine LTs

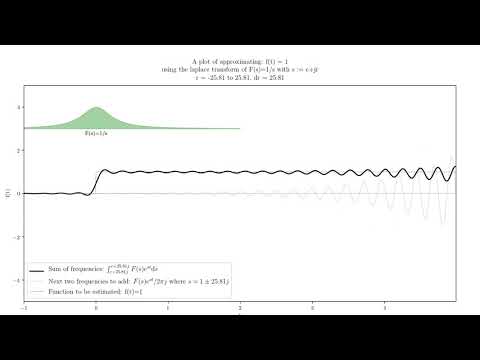
Do you want to understand the visual meaning of the Laplace Transform? In this video series on the Laplace Transform, I explain graphical interpretations (visual explanations) in addition to symbolic calculations, both for basic examples and for theoretical results, as well as study applications to ordinary differential equations. I review the Laplace transform definition and qualitative properties when f(t) is non-negative. I make observations about what might happen for functions which oscillate between positive and negative values. I also talk about how the Laplace transform is used to solve differential equation initial value problems (ODE IVPs), based on linearity. Finally, I symbolically compute and graphically analyze the Laplace Transform for three fundamental examples: the unite step function (with jump discontinuity at t = a), the exponential function e^(a*t), and the cosine function cos(w*t).

Laplace Transform Visually Explained, Part 2. (a.k.a. Introduction to the Laplace Transform, Part 2).

#laplacetransform #laplacetransformexplained #laplacetransformvisualization

AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.

[michaeldevilangel]

This is really cool. Any chance you could do some interesting vids on nonlinear differential equations (post grad level) ?

[hebelehubele]

The investment of 1000 euros gives 1010 if kept for 6 months, 1020 if kept for one year. Comparing the annual compound interest rates of the two alternatives, (a) investing for six months is better. - (b)investing for one year is better. - (c) the two alternatives are aquivalent. - (d) it is impossiable to say which alternative is better