Proper closed subspace of H , is orthogonal to non zero vector of H, Inner product space

Показать описание

#msc #maths #properclosed #subspace #hilbertspace #nonzerovector #innerproductspace #concept #ips

billionaire icon

Рекомендации по теме

Комментарии

It is very very very helpful ma'am Thank you very much ma'am 🤗🙏🙏

maliksahu

Madam, please share this proof 👇👇👇👇
Let M be a closed linear subspace then for each x in H there is a unique element in M closed to x being the projection of x onto M denoted px and characterized by the fact that ( x- Px, m)= 0 for every m in M also P is linear map

minakshibhagat

Bhut acha smjhaya h lekin board pe sbse neeche jo likha h vo dikh ni ra
Halanki sunai b de rha h lekin phir b complete board dikhna chiye
Aur dusri baat ki aap shuru me toh shi likhte ho phir baad me bhut chota likhne lgte ho mtlb font chota hota chala jata h
In do baaton pe dhyan dijiye plz
well, teaching is gud🙏

AshwiniTanwar

Ma'am plss projection theorem ko upload kr dijiye as soon as 🙏🙏🙏

maliksahu

Ma'am subscriber ni badh rahe hai kahke padhana mat chhodiyega kyoki AAP bhut achcha padhati ho ma'am Thank u very much ma'am 🙏🙏🙏

maliksahu

Proper closed subspace of H , is orthogonal to non zero vector of H, Inner product space

Proper closed subspace of H , is orthogonal to non zero vector of H, Inner product space

IF M IS A PROPER CLOSED SUBSPACE OF H, THEN THERE EXIST Zo IN H s.t. Zo ORTHOGONAL TO M FOR MSC

Orthogonal complement of a non empty subset of H is a closed linear subspace of H, IPS

if M is a linear subspace of a hilbert space h show that m is closed m.sc. mathematics solution by k

How to Prove a Set is a Subspace of a Vector Space

Functional Analysis mathematics //Theorem proof-A subspace of Hilbert Space is closed iff ...

if m and n are closed linear subspaces of a hilbert space h such that M perpendicular to n

Eigen Space invariant under T and closed linear subspace of H | by Sapna | @billionaireicon3311

orthogonal complement theorem best on orthogonal complement MSc maths solution by Khushboo Jafri

L-84||Theorem || Inner product space || Hilbert space || M.Sc. Mathematics || Nivaanmath Academy

Functional Analysis - 38:M+N is closed sub space in the Hilbert space H

L-85||Theorem|| Inner product space || Hilbert space || M.Sc. Mathematics

closed subspace M of Hilbert space contains unique vector such that ||x- y||=d , y is vector in M

A Set Fails to be a Subspace of a Vector Space

Closed, convex subpace of hilbert space contains a unique vector of smallest norm , IPS

9.2 - Hilbert spaces - Part 2

Ursula Molter, Best 'good' subspace data fitting, 2023.02.07

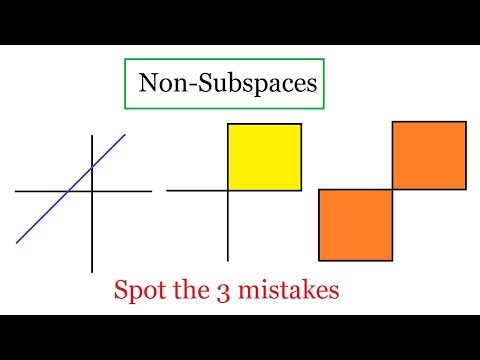
Not subspace

MATH224-LEC28: Vector Spaces - Subspace Part 2

Determine if a set is closed under scalar multiplication | Linear algebra I

Closed Subspaces of Reflexive Spaces

Tricks to determine whether a given subset of R^n is a subspace or not.

Hilbert Spaces: separable Hilbert Spaces, orthogonality theorems, 3-10-23 part 2

Hilbert Space Lec.-6